题目内容
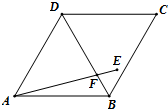如图，在菱形ABCD中，∠BAD=60°，AB=4，E是△BCD内部任意一点，AE与BD交于点F，则| AF |
| BF |
分析：根据已知条件，设
=t
+（1-t）
，0＜t＜1，则
=
-
=（1-t）（
-
），由此利用配方法能求出
•
的最小值．
| AF |
| AB |
| AD |
| BF |
| AF |
| AB |
| AD |
| AB |
| AF |
| BF |
解答：解：∵在菱形ABCD中，∠BAD=60°，AB=4，
∴
•
=|
|×|
|×cos60°=4×4×
=8，
|
|2 =|
|2=16，
设
=t
+（1-t）
，0＜t＜1，
则
=
-
=（1-t）（
-
），
∴
•
=（1-t）[t
+（1-t）
]（
-
）
=（1-t）[（1-t）
2-t
2+（2t-1）
•
]
=（1-t）[16（1-2t）+8（2t-1）]
=16（1-t）（
-t）
=16（t-
）2-1≥-1，
∴
•
的最小值是-1．
故答案为：-1．
∴
| AB |
| AD |
| AB |
| AD |
| 1 |
| 2 |
|
| AB |
| AD |
设
| AF |
| AB |
| AD |
则
| BF |
| AF |
| AB |
| AD |
| AB |
∴
| AF |
| BF |
| AB |
| AD |
| AD |
| AB |
=（1-t）[（1-t）
| AD |
| AB |
| AB |
| AD |
=（1-t）[16（1-2t）+8（2t-1）]
=16（1-t）（
| 1 |
| 2 |
=16（t-
| 3 |
| 4 |
∴
| AF |
| BF |
故答案为：-1．
点评：本题考查向量数量积的最小值的求法，是中档题，解题时要注意数形结合思想的合理运用．
练习册系列答案
步步高达标卷系列答案
相关题目
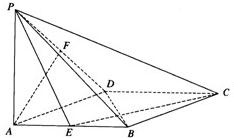如图，在菱形ABCD中，∠DAB=60°，PA⊥底面ABCD，且PA=AB=2，E、F分别是AB与PD的中点．
如图，在菱形ABCD中，MA⊥平面ABCD，且四边形ADNM是平行四边形．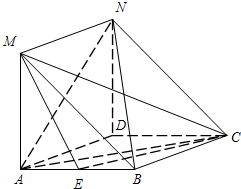
如图，在菱形ABCD中，∠DAB=60°，E是AB的中点，MA⊥平面ABCD，且在矩形ADNM中，AD=2，
（2012•大丰市一模）如图，在菱形ABCD中，E是AB的中点，且DE⊥AB．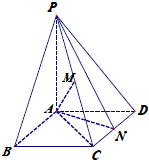
如图，在菱形ABCD中，∠BAD=120°，点N为CD中点，PA⊥平面ABCD．