题目内容
设 与
与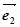 是两个单位向量,其夹角为60°,且
是两个单位向量,其夹角为60°,且 ,
,
(1)求
(2)分别求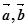 的模;
的模;
(3)求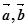 的夹角。
的夹角。
(1) ;(2)
;(2) ;(3)
;(3)
解析试题分析:(1)根据向量的数量积公式和运算律展开,即可求值;
(2) ,然后根据向量的数量积公式展开;
,然后根据向量的数量积公式展开;
(3)根据向量的夹角公式 ,代入前两问的结果,即可求出夹角.
,代入前两问的结果,即可求出夹角.
解:(1)a·b==(2e1+e2)·(-3e1+2e2,)=-6e12+ e1·e2+2e22=- ,(4分)
,(4分)
(2)∵a=2e1+e2,∴|a|2=a2=(2e1+e2)2=4e12+4e1·e2+e22=7,∴|a|= 。(6分)
。(6分)
同理得|b|= 。(8分)
。(8分)
(3)设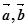 的夹角为
的夹角为 。则 cosθ=
。则 cosθ= (7分)
(7分)
=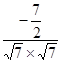 =-
=- , (10分)
, (10分)
∴θ=120°、 (12分)
考点:1.向量的数量积公式;2.运算律;3.模与夹角公式.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 中,动点
中,动点 到两点
到两点 、
、 的距离之和等于4.设点
的距离之和等于4.设点 .
. 与
与 、
、 两点,若
两点,若 ,求
,求 的值.
的值. 为坐标原点,
为坐标原点,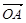 =(
=( ),
),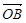 =(1,
=(1, ),
),  .
. 的定义域为[-
的定义域为[- ,
,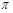 ],求y=
],求y= 的值.
的值. ,向量
,向量 与向量
与向量 的夹角为
的夹角为 ,且
,且 求向量
求向量 ,向量
,向量 ,其中
,其中 ,若
,若 试求
试求 的取值范围.
的取值范围. ,
, ,且
,且 与
与 夹角为
夹角为 .求:
.求: ;
; 的夹角.
的夹角. 是两个不共线的非零向量,且
是两个不共线的非零向量,且 .
.  当实数t为何值时,
当实数t为何值时,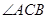 为钝角?
为钝角? ,求
,求 的值域及单调递减区间.
的值域及单调递减区间. ,其中
,其中 .
. 与
与 互相垂直;
互相垂直; 与
与 (
( )的长度相等,求
)的长度相等,求 .
. (2α-β)=1,则α与β的夹角的余弦值为 .
(2α-β)=1,则α与β的夹角的余弦值为 .