题目内容
已知 ,
, ,且
,且 与
与 夹角为
夹角为 .求:
.求:
(1) ;
;
(2) 与
与 的夹角.
的夹角.
(1) ;(2)
;(2) .
.
解析试题分析:先由题中条件得到 ,再由
,再由 ,代入数值,计算得到
,代入数值,计算得到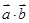 的值.(1)由平面向量的数量积的运算法则得到
的值.(1)由平面向量的数量积的运算法则得到 ,代入数值即可得到结果;(2)先计算
,代入数值即可得到结果;(2)先计算 ,
, 的值,然后再由向量夹角的计算公式
的值,然后再由向量夹角的计算公式 (设
(设 与
与 的夹角为
的夹角为 )得到
)得到 ,结合
,结合 即可得出
即可得出 的值.
的值.
试题解析:由题意可得 ,
, ,
,
(1)
(2)设 与
与 的夹角为
的夹角为
因为 ,
,
所以
又 ,所以
,所以 ,
, 与
与 的夹角为
的夹角为 .
.
考点:平面向量的数量积.

练习册系列答案
相关题目
 ,
, ,且
,且 与夹角为
与夹角为 ,求
,求 ;
; 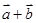 的夹角
的夹角 与
与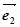 是两个单位向量,其夹角为60°,且
是两个单位向量,其夹角为60°,且 ,
,
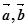 的模;
的模; ,
, ,对任意
,对任意 都有
都有 .
. 的最小值;
的最小值; ,使
,使
 sin2x+a)(x∈R,a∈R,a是常数),且y=
sin2x+a)(x∈R,a∈R,a是常数),且y= ·
· (O为坐标原点).
(O为坐标原点). ]时,f(x)的最大值为2013,求a的值.
]时,f(x)的最大值为2013,求a的值. ,求
,求 的值。
的值。 ,
, ,已知函数
,已知函数 在
在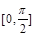 上的最大值为6.
上的最大值为6. 的值;
的值; ,
, .求
.求 的值.
的值. ,且
,且 与
与 的夹角为120°.
的夹角为120°. ; (2)
; (2)  ; (3)
; (3)  .
. ,且|b|=4,(a+2b)·(a-3b)=-72, 则向量|a|=
,且|b|=4,(a+2b)·(a-3b)=-72, 则向量|a|=