题目内容
已知 为坐标原点,
为坐标原点,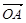 =(
=( ),
),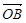 =(1,
=(1, ),
),  .
.
(1)若 的定义域为[-
的定义域为[- ,
,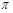 ],求y=
],求y= 的单调递增区间;
的单调递增区间;
(2)若 的定义域为[
的定义域为[ ,
,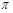 ],值域为[2,5],求
],值域为[2,5],求 的值.
的值.
(1)[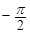 ,
, ],[
],[ ,
, ] (2)m=1
] (2)m=1
解析试题分析:(1)先利用向量的数量积公式计算出f(x),然后利用降幂公式、辅助角公式化简得到f(x)
= ,进而得到单调区间.(2)找到定义域与值域的对应关系,然后解方程组.
,进而得到单调区间.(2)找到定义域与值域的对应关系,然后解方程组.
(1)∵ =
=
= =
= (4分)
(4分)
由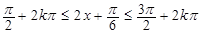 (k∈Z),
(k∈Z),
得 在
在 上的单调递增区间为
上的单调递增区间为 (k∈Z),
(k∈Z),
(其它情况可酌情给分)
又 的定义域为[-
的定义域为[- ,
,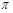 ],
],
∴ 的增区间为:[
的增区间为:[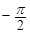 ,
, ],[
],[ ,
, ] (7分)
] (7分)
(2)当 ≤x≤
≤x≤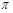 时,
时, ,∴
,∴ ,
,
∴1+m≤ ≤4+m,∴
≤4+m,∴
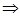 m=1 (13分)
m=1 (13分)
考点:向量的数量积的坐标表示;两角和的正弦公式;正弦函数的单调性以及值域.

练习册系列答案
相关题目

 ,
, ,
,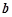
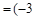 ,
, .
. 与
与 的夹角;
的夹角;

 ,求实数
,求实数 的值.
的值. ,
, ,且
,且 与夹角为
与夹角为 ,求
,求 ;
; 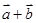 的夹角
的夹角 ,
, ,其中
,其中 ,
, ,
, 及
及 的值;
的值; 与
与 的夹角的正弦值.
的夹角的正弦值. 与
与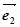 是两个单位向量,其夹角为60°,且
是两个单位向量,其夹角为60°,且 ,
,
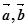 的模;
的模; ,
, ,对任意
,对任意 都有
都有 .
. 的最小值;
的最小值; ,使
,使
 ,求
,求 的值。
的值。 =
= ,
,  =
=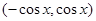 ,
,  =
=
 ,求向量
,求向量 时,求函数
时,求函数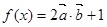 的最大值
的最大值