题目内容
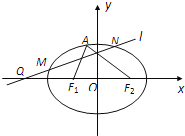
【题目】已知椭圆![]() 过点
过点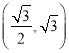 ,离心率为
,离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆的上顶点作直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,
两点, ![]() 为原点.
为原点.
①求证: ![]() ;
;
②设![]() 、
、![]() 分别与椭圆相交于
分别与椭圆相交于![]() 、
、![]() 两点,过原点
两点,过原点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,证明:
,证明: ![]() 为定值.
为定值.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)根据椭圆过定点以及椭圆的离心率可得 ,解得
,解得![]() 的值,由椭圆的定义可得
的值,由椭圆的定义可得![]() 的值,将
的值,将![]() 的值代入椭圆方程即可得答案;(2)①设过椭圆的上顶点
的值代入椭圆方程即可得答案;(2)①设过椭圆的上顶点![]() 的直线的
的直线的![]() 方程为
方程为![]() ,与抛物线方程联立,设出
,与抛物线方程联立,设出![]() 点的坐标,由根与系数的关系分析计算
点的坐标,由根与系数的关系分析计算![]() 的值,由向量数量积的性质可得证明;②直线
的值,由向量数量积的性质可得证明;②直线![]() 与抛物线联立,由韦达定理及平面向量数量积公式可得,
与抛物线联立,由韦达定理及平面向量数量积公式可得, ![]() 的等量关系,结合点到直线距离公式可得结果.
的等量关系,结合点到直线距离公式可得结果.
试题解析:(1) ![]() ,所以
,所以![]() ,又
,又![]() ,解得
,解得![]() ,
,![]() ,
,
所以椭圆的方程为![]()
(2)①证明:设![]() 、
、![]() ,依题意,直线
,依题意,直线![]() 一定有斜率
一定有斜率![]() ,
, ![]() 的方程为
的方程为![]() ,
,
联立方程![]() 消去
消去![]() 得
得 ![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,![]()
②证明:设![]() 、
、![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,![]() ,联立方程
,联立方程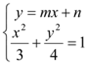 消去
消去![]() 得
得 ![]() ,
,
![]() ,
,![]() ,
,
而![]()
由![]() 得
得
![]() ,即
,即![]()
 . 所以
. 所以![]() 为定值.
为定值.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目