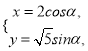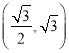题目内容
【题目】已知椭圆
： 
，曲线
上的动点
满足：
.
（1）求曲线
的方程；
（2）设
为坐标原点，第一象限的点
分别在
和
上， 
，求线段
的长.
【答案】(1) 
;(2) 
.
【解析】试题分析:(1) 由已知，动点
到点
， 
的距离之和为
，且
，根据椭圆的定义求出曲线的方程;(2) 
两点的坐标分别为
，由
及（1）知， 
三点共线且点
不在
轴上，因此可设直线
的方程为
,分别联立直线AB与曲线
和
,得出点A,B的坐标,根据两点间的距离公式求出弦长即可.
试题解析:
（1）由已知，动点
到点
， 
的距离之和为
，
且
，所以动点
的轨迹为椭圆，而
， 
，所以
，
故椭圆
的方程为
.
（2）解： 
两点的坐标分别为
，由
及（1）知， 
三点共线且点
不在
轴上，因此可设直线
的方程为
.
将
代入
中，得
，所以
，
将
代入
中，得
，所以
，
又由
，得
，即
，
解得
，
故
.
练习册系列答案
相关题目
【题目】某社区超市购进了A,B,C,D四种新产品，为了解新产品的销售情况，该超市随机调查了15位顾客（记为
）购买这四种新产品的情况，记录如下（单位：件）：
顾 客 产 品 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A | 1 | 1 | 1 | 1 | 1 | ||||||||||
B | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
C | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
D | 1 | 1 | 1 | 1 | 1 | 1 |
（Ⅰ）若该超市每天的客流量约为300人次，一个月按30天计算，试估计产品A的月销售量（单位：件）；
（Ⅱ）为推广新产品，超市向购买两种以上（含两种）新产品的顾客赠送2元电子红包.现有甲、乙、丙三人在该超市购物，记他们获得的电子红包的总金额为X，
求随机变量X的分布列和数学期望；
（Ⅲ）若某顾客已选中产品B，为提高超市销售业绩，应该向其推荐哪种新产品？（结果不需要证明）
