题目内容
 如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.
如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.(1)求实数b的值;
(11)求以点A为圆心,且与抛物线C的准线相切的圆的方程.
分析:(I)由
,得x2-4x-4b=0,由直线l与抛物线C相切,能求出b.
(II)由b=-1,得x2-4x+4=0,解得x=2,将其代入x2=4y,得y=1,故点A(2,1).因为圆A与抛物线C的准线相切,所以圆心A到抛物线C的准线y=-1的距离等于圆A的半径r,由此能求出圆A的方程.
|
(II)由b=-1,得x2-4x+4=0,解得x=2,将其代入x2=4y,得y=1,故点A(2,1).因为圆A与抛物线C的准线相切,所以圆心A到抛物线C的准线y=-1的距离等于圆A的半径r,由此能求出圆A的方程.
解答:解:(I)由
,得x2-4x-4b=0,(*)
因为直线l与抛物线C相切,
所以△=(-4)2-4×(-4b)=0,
解得b=-1.…(4分)
(II)由(I)知b=-1,
故方程(*)即为x2-4x+4=0,
解得x=2,将其代入x2=4y,
得y=1,故点A(2,1).
因为圆A与抛物线C的准线相切,
所以圆心A到抛物线C的准线y=-1的距离等于圆A的半径r,
即r=|1-(-1)|=2,
所以圆A的方程为(x-2)2+(y-1)2=4.…..(12分)
|
因为直线l与抛物线C相切,
所以△=(-4)2-4×(-4b)=0,
解得b=-1.…(4分)
(II)由(I)知b=-1,
故方程(*)即为x2-4x+4=0,
解得x=2,将其代入x2=4y,
得y=1,故点A(2,1).
因为圆A与抛物线C的准线相切,
所以圆心A到抛物线C的准线y=-1的距离等于圆A的半径r,
即r=|1-(-1)|=2,
所以圆A的方程为(x-2)2+(y-1)2=4.…..(12分)
点评:本题考查满足条件的实数值的求法,考查圆的方程的求法.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.
如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.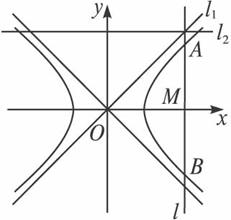
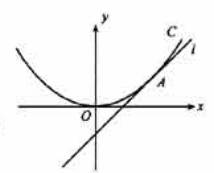
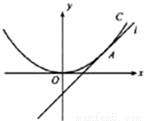 如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.
如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.