题目内容
（本小题满分12分）
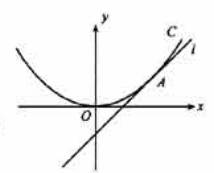
如图，直线l：y=x+b与抛物线C：x2=4y相切于点A。
（I）求实数b的值；
（11）求以点A为圆心，且与抛物线C的准线相切的圆的方程．
 |
本小题主要考查直线、圆、抛物线等基础知识，考查运算求解能力，考查函数与方程思想、数形结合思想，满分12分。
解：（I）由
，（*）
因为直线
与抛物线C相切，所以
解得b=-1。
（II）由（I）可知
，
解得x=2，代入
故点A（2，1），
因为圆A与抛物线C的准线相切，
所以圆A的半径r等于圆心A到抛物线的准线y=-1的距离，
即
所以圆A的方程为
练习册系列答案
阅读快车系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
