题目内容
3.在等边△ABC中,M为△ABC内一动点,∠BMC=120°,则$\frac{MA}{MC}$的最小值是( )| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 如图所示,不妨设等边△ABC的边长为2,M为△ABC内一动点,∠BMC=120°.点M在弦BC所对的弓形$\widehat{BMC}$上,∠BQC=120°.由图可知:当点M取与y轴的交点时,∠MBC=30°,可得:Q$(0,-\frac{\sqrt{3}}{3})$,A$(0,\sqrt{3})$,C(1,0),M(x,y).设参数方程为:$\left\{\begin{array}{l}{x=\frac{2\sqrt{3}}{3}cosθ}\\{y=-\frac{\sqrt{3}}{3}+\frac{2\sqrt{3}}{3}sinθ}\end{array}\right.$,$\frac{|MA{|}^{2}}{|MC{|}^{2}}$=$\frac{{x}^{2}+(y-\sqrt{3})^{2}}{(x-1)^{2}+{y}^{2}}$=$\frac{5-4sinθ}{2-\sqrt{3}cosθ-sinθ}$=t,化为:sin(θ+β)=$\frac{5-2t}{\sqrt{(4-t)^{2}+(\sqrt{3}t)^{2}}}$≤1,解出即可得出.
解答 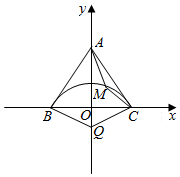 解:如图所示,
解:如图所示,
不妨设等边△ABC的边长为2,
∵M为△ABC内一动点,∠BMC=120°,
∴点M在弦BC所对的弓形$\widehat{BMC}$上,∠BQC=120°.
由图可知:当点M取与y轴的交点时,∠MBC=30°,
可得:Q$(0,-\frac{\sqrt{3}}{3})$,A$(0,\sqrt{3})$,C(1,0),M(x,y).
点M所在圆的方程为:${x}^{2}+(y+\frac{\sqrt{3}}{3})^{2}$=$\frac{4}{3}$.
设参数方程为:$\left\{\begin{array}{l}{x=\frac{2\sqrt{3}}{3}cosθ}\\{y=-\frac{\sqrt{3}}{3}+\frac{2\sqrt{3}}{3}sinθ}\end{array}\right.$,
∴$\frac{|MA{|}^{2}}{|MC{|}^{2}}$=$\frac{{x}^{2}+(y-\sqrt{3})^{2}}{(x-1)^{2}+{y}^{2}}$=$\frac{\frac{4}{3}co{s}^{2}θ+(-\frac{4\sqrt{3}}{3}+\frac{2\sqrt{3}}{3}sinθ)^{2}}{(\frac{2\sqrt{3}}{3}cosθ-1)^{2}+(-\frac{\sqrt{3}}{3}+\frac{2\sqrt{3}}{3}sinθ)^{2}}$=$\frac{5-4sinθ}{2-\sqrt{3}cosθ-sinθ}$=t,
化为:sin(θ+β)=$\frac{5-2t}{\sqrt{(4-t)^{2}+(\sqrt{3}t)^{2}}}$≤1,
解得t≥$\frac{3}{4}$,
∴$\frac{|MA|}{|MC|}$$≥\frac{\sqrt{3}}{2}$.
故选:C.
点评 本题考查了等边三角形的性质、圆的性质、直角三角形的边角关系、三角函数的单调性、和差公式,考查了推理能力与计算能力,属于中档题.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案 据报我国正分别在大连和上海建造两航母,而建造航母必需特种钢.为建造航母的需要,要将两种不同的特种钢板截成A、B、C三种规格,每张钢板可同时截成三种规格的小钢板的块数如下表所示:
据报我国正分别在大连和上海建造两航母,而建造航母必需特种钢.为建造航母的需要,要将两种不同的特种钢板截成A、B、C三种规格,每张钢板可同时截成三种规格的小钢板的块数如下表所示:| 规格类型 钢板类型 | A规格 | B规格 | C规格 |
| 第一种钢板 | 2 | 1 | 1 |
| 第二种钢板 | 1 | 2 | 3 |