题目内容
如图,已知Rt△BCD的一条直角边BC与等腰Rt△ABC的斜边BC重合,若AB=2,∠CBD=30°, ,则m-n= .
,则m-n= .
【答案】分析:由条件求得BC 的值、及∠ACD的值,建立坐标系,求得A、B、C、D的坐标,根据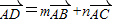 ,求出m和n的值,即可求得m-n的值.
,求出m和n的值,即可求得m-n的值.
解答: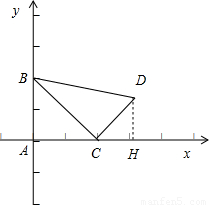 解:由题意可得BC=
解:由题意可得BC=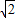 AB=2
AB=2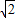 ,CD=BC•tan∠CBD=2
,CD=BC•tan∠CBD=2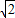 tan30°=
tan30°=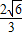 ,
,
∠ACD=45°+90°=135°.
以 AC所在的直线为x轴,以AB所在的直线为y轴,建立坐标系,如图:
作DH⊥x轴,H为垂足,
则CH=CDcos(180°-135°)=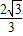 ,DH=CDsin(180°-135°)=
,DH=CDsin(180°-135°)=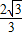 .
.
故D(2+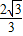 ,
,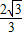 ),再由题意可得B(0,2),C(2,0).
),再由题意可得B(0,2),C(2,0).
∵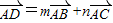 ,
,
∴(2+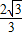 ,
,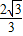 )=m(0,2)+n(2,0)=(2n,2m),
)=m(0,2)+n(2,0)=(2n,2m),
∴2+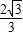 =2n,
=2n,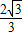 =2m,∴m=
=2m,∴m=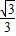 ,n=1+
,n=1+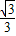 ,∴m-n=-1,
,∴m-n=-1,
故答案为-1.
点评:本题主要考查平面向量基本定理及其几何意义,求出m和n的值,是解题的关键,属于中档题.
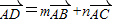 ,求出m和n的值,即可求得m-n的值.
,求出m和n的值,即可求得m-n的值.解答:
 解:由题意可得BC=
解:由题意可得BC=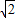 AB=2
AB=2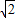 ,CD=BC•tan∠CBD=2
,CD=BC•tan∠CBD=2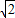 tan30°=
tan30°=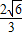 ,
,∠ACD=45°+90°=135°.
以 AC所在的直线为x轴,以AB所在的直线为y轴,建立坐标系,如图:
作DH⊥x轴,H为垂足,
则CH=CDcos(180°-135°)=
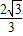 ,DH=CDsin(180°-135°)=
,DH=CDsin(180°-135°)=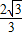 .
.故D(2+
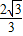 ,
,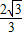 ),再由题意可得B(0,2),C(2,0).
),再由题意可得B(0,2),C(2,0).∵
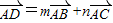 ,
,∴(2+
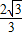 ,
,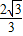 )=m(0,2)+n(2,0)=(2n,2m),
)=m(0,2)+n(2,0)=(2n,2m),∴2+
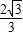 =2n,
=2n,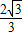 =2m,∴m=
=2m,∴m=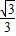 ,n=1+
,n=1+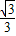 ,∴m-n=-1,
,∴m-n=-1,故答案为-1.
点评:本题主要考查平面向量基本定理及其几何意义,求出m和n的值,是解题的关键,属于中档题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD=
如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD= (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (A)(不等式选做题)不等式|x+1|-|x-2|>2的解集为
(A)(不等式选做题)不等式|x+1|-|x-2|>2的解集为 (A)(几何证明选讲选做题)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为=
(A)(几何证明选讲选做题)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为= (2013•汕头二模)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC边为直径与AB交于点D,则三角形ACD的面积为
(2013•汕头二模)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC边为直径与AB交于点D,则三角形ACD的面积为