Question

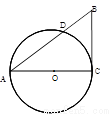
（A）（几何证明选讲选做题）如图，已知Rt△ABC的两条直角边AC，BC的长分别为3cm，4cm，以AC为直径作圆与斜边AB交于点D，则BD的长为=

16

5

；
（B）（不等式选讲选做题）关于x的不等式|x-1|+|x-2|≤a²+a+1的解集为空集，则实数a的取值范围是

（-1，0）

；
（C）（坐标系与参数方程选做题）已知极坐标的极点在直角坐标系的原点O处，极轴与x轴的正半轴重合，曲线C的参数方程为

x=3cosθ y=sinθ

（θ为参数），直线l的极坐标方程为ρcos(θ-

π

3

)=6．点P在曲线C上，则点P到直线l的距离的最小值为

6-

3

．

Answer 1

分析：本题中（A）是几何证明选讲题，由已知条件AC=3，BC=4，可求出AB=5，只要连接CD，可得到两个相似的直角三角形，根据相似三角形对应边成比例可求BD的长；
（B）是不等式选讲题，不等式右侧含有待求系数，可考虑不等式左边绝对值的几何意义，理解为数轴上的动点到两定点的距离问题，求出不等式左边的范围，只要右侧小于这个范围就可以求出a的范围；
（C）是参数方程与极坐标问题，首先把参数方程和极坐标方程转化为普通方程，问题变为了求椭圆上的动点到直线上点的最小值．

解答：解：（A）连接CD，因直径所对圆周角为直角，所以∠CDB为直角，则Rt△BDC∽Rt△BCA，
根据相似三角形对应边成比例，则

BC

BD

=

AB

BC

，所以BD=

BC2

AB

=

16

5

．
（B）不等式|x-1|+|x-2|≤a²+a+1的左边的几何意义为数轴的动点X到两实数1、2对应点的距离，所以|x-1|+|x-2|≥1，要使原不等式的解集为空集，只需a²+a+1＜1即可，
解得-1＜a＜0，所以使关于x的不等式|x-1|+|x-2|≤a²+a+1的解集为空集的实数a的取值范围
是（-1，0）．
（C）由曲线C的参数方程为

x=3cosθ y=sinθ

（θ为参数），知曲线C的普通方程为

x2

9

+y2=1直线l的极坐标方程为ρcos(θ-

π

3

)=6，知直线l方程为x+

3

y-12=0，设与直线l平行的直线方程为x+

3

y+m=0，
联立

x2 9 +y2=1 x+ 3 y+m=0

得12y2+2

3

my+m2-9=0，由△=0，得m=-2

3

，两平行线x+

3

y-12=0和
x+

3

y-2

3

=0间的距离即为点P到直线l的距离的最小值，由两平行线距离公式得

|-12-2 3 |

12+( 3 )2

=6-

3

．
故A、B、C答案分别为

16

5

、（-1，0）、6-

3

．

点评：几何证明选讲问题当属平面几何内容，解决问题的关键是做好有效的辅助线；含绝对值的不等式的解法，若是单纯的求解，可分段讨论，涉及待求系数问题，考虑绝对值的几何意义不失为一种有效的解题方法；
参数方程与极坐标问题，要考虑转化为常见的普通方程求解．