题目内容
20.已知命题p:方程x2+my2=2表示焦点在y轴上的椭圆,命题q:不等式4x2+4(m-2)x+1>0在x∈R上恒成立,又p∨q为真,?q为真,求实数m的取值范围.分析 先求出命题为真命题的等价条件,然后根据复合命题真假之间的关系建立条件关系即可.
解答 解:∵p∨q为真,?q为真,
∴q为假命题,p是真命题,
若方程x2+my2=2表示焦点在y轴上的椭圆,
则等价为方程$\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{\frac{2}{m}}$=1表示焦点在y轴上的椭圆,
即$\frac{2}{m}$>2,解得0<m<1,即p:0<m<1,
不等式4x2+4(m-2)x+1>0在x∈R上恒成立,
则判别式△=16(m-2)2-16<0,
即(m-2)2<1,解得1<m<3,即q:1<m<3,¬q:m≥3或m≤1,
则$\left\{\begin{array}{l}{0<m<1}\\{m≥3或m≤1}\end{array}\right.$,解得0<m<1,
即实数m的取值范围是(0,1).
点评 本题主要考查复合命题的真假关系的判断和应用,根据条件求出命题的等价条件是解决本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
8.如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥与外接球的体积比为( )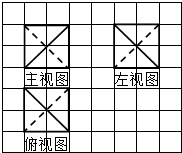

| A. | $\frac{2\sqrt{3}}{9π}$ | B. | $\frac{\sqrt{3}}{9π}$ | C. | $\frac{\sqrt{2}}{16π}$ | D. | $\frac{8\sqrt{2}}{π}$ |
15.函数f(x)=5sin($\frac{x}{3}$-$\frac{π}{10}$)(x∈R)的最大值和最小正周期分别是( )
| A. | 5,2π | B. | 1,6π | C. | 1,2π | D. | 5,6π |
5.直线x-4y+12=0在x轴和y轴的截距分别是( )
| A. | 12,3 | B. | -12,-3 | C. | 12,-3 | D. | -12,3 |