题目内容
7．已知向量$\overrightarrow{a}$=（2，0）与$\overrightarrow{b}$=（1，-2），求|2$\overrightarrow{a}$-$\overrightarrow{b}$|分析 运用向量的加减运算，求得2$\overrightarrow{a}$-$\overrightarrow{b}$=（3，2），再由向量模的公式，计算即可得到所求值．
解答 解：由向量$\overrightarrow{a}$=（2，0）与$\overrightarrow{b}$=（1，-2），
可得2$\overrightarrow{a}$-$\overrightarrow{b}$=（4，0）-（1，-2）=（3，2），
即有|2$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$．
点评 本题考查向量的模的求法，注意运用向量的坐标运算，考查运算能力，属于基础题．
练习册系列答案
相关题目
15．在倾斜角等于30°的山坡上竖立一根旗杆，当太阳在山顶上方时，从山脚看太阳的仰角是60°，旗杆此时在山坡上的影子长是25米，则旗杆高为（ ）
| A． | 25米 | B． | 12.5米 | C． | 22米 | D． | 30米 |
19．设F1、F2是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+${\frac{{y}^{2}}{{b}^{2}}}^{\;}$=1（a＞b＞0）的左右焦点，P为直线x=$\frac{5a}{4}$上一点，△F2PF1是底角为30°的等腰三角形，则椭圆C的离心率为（ ）
| A． | $\frac{5}{8}$ | B． | $\frac{\sqrt{10}}{4}$ | C． | $\frac{3}{4}$ | D． | $\frac{\sqrt{3}}{2}$ |
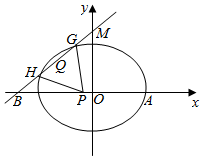已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$过点A（2，0），离心率$e=\frac{1}{2}$，斜率为k（0＜k≤1）直线l过点M（0，2），与椭圆C交于G，H两点（G在M，H之间），与x轴交于点B．