题目内容
椭圆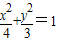 上有n个不同的点P1,P2,…,Pn,椭圆的右焦点为F,数列{|PnF|}是公差大于
上有n个不同的点P1,P2,…,Pn,椭圆的右焦点为F,数列{|PnF|}是公差大于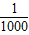 的等差数列,则n的最大值是( )
的等差数列,则n的最大值是( )A.2000
B.2001
C.2003
D.2005
【答案】分析:设P(xn,yn),P到右准线的距离为dn,由圆锥曲线的统一定义算出|PnF|=2- xn,结合题意数列{|PnF|}是公差大于
xn,结合题意数列{|PnF|}是公差大于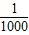 的等差数列,得出关于横坐标x1、xn的不等式,再利用椭圆上点的横坐标范围,解之即可得到n的取值范围,从而得出n的最大值.
的等差数列,得出关于横坐标x1、xn的不等式,再利用椭圆上点的横坐标范围,解之即可得到n的取值范围,从而得出n的最大值.
解答:解:求得椭圆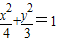 的a=2,b=
的a=2,b=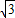 ,c=1
,c=1
右焦点为F(1,0),离心率e=
设P(xn,yn),P到右准线x=4的距离为dn,
根据圆锥曲线的统一定义,得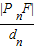 =e=
=e=
∴|PnF|= dn=
dn= (4-xn)=2-
(4-xn)=2- xn,
xn,
∵数列{|PnF|}是公差大于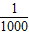 的等差数列,
的等差数列,
∴|PnF|-|P1F|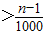 ,可得
,可得 x1-
x1- xn
xn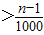
化简得x1-xn>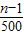 ,
,
结合椭圆上点的横坐标的范围,得x1-xn<2a=4
∴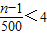 ,得n<2001,得n的最大值为2000
,得n<2001,得n的最大值为2000
故选:A
点评:本题给出椭圆上的n个点,在焦半径成公差大于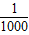 的等差数列情况下,求n的最大值.着重考查了椭圆的几何性质、等差数列的通项公式等知识,属于中档题.
的等差数列情况下,求n的最大值.着重考查了椭圆的几何性质、等差数列的通项公式等知识,属于中档题.
 xn,结合题意数列{|PnF|}是公差大于
xn,结合题意数列{|PnF|}是公差大于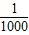 的等差数列,得出关于横坐标x1、xn的不等式,再利用椭圆上点的横坐标范围,解之即可得到n的取值范围,从而得出n的最大值.
的等差数列,得出关于横坐标x1、xn的不等式,再利用椭圆上点的横坐标范围,解之即可得到n的取值范围,从而得出n的最大值.解答:解:求得椭圆
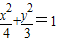 的a=2,b=
的a=2,b=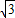 ,c=1
,c=1右焦点为F(1,0),离心率e=

设P(xn,yn),P到右准线x=4的距离为dn,
根据圆锥曲线的统一定义,得
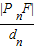 =e=
=e=
∴|PnF|=
 dn=
dn= (4-xn)=2-
(4-xn)=2- xn,
xn,∵数列{|PnF|}是公差大于
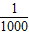 的等差数列,
的等差数列,∴|PnF|-|P1F|
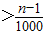 ,可得
,可得 x1-
x1- xn
xn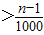
化简得x1-xn>
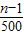 ,
,结合椭圆上点的横坐标的范围,得x1-xn<2a=4
∴
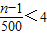 ,得n<2001,得n的最大值为2000
,得n<2001,得n的最大值为2000故选:A
点评:本题给出椭圆上的n个点,在焦半径成公差大于
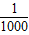 的等差数列情况下,求n的最大值.着重考查了椭圆的几何性质、等差数列的通项公式等知识,属于中档题.
的等差数列情况下,求n的最大值.着重考查了椭圆的几何性质、等差数列的通项公式等知识,属于中档题. 
练习册系列答案
相关题目
 上有n个不同的点:P1,P2,
,Pn,椭圆的右焦点为F,数列{|PnF|}是公差大于
上有n个不同的点:P1,P2,
,Pn,椭圆的右焦点为F,数列{|PnF|}是公差大于 的等差数列,则n的最大值是 ( )
的等差数列,则n的最大值是 ( ) 上有n个不同的点:P1 ,P2 ,…,Pn
, 椭圆的右焦点为F,数列{|PnF|}是公差大于
上有n个不同的点:P1 ,P2 ,…,Pn
, 椭圆的右焦点为F,数列{|PnF|}是公差大于 的等差数列, 则n的最大值是(
)
的等差数列, 则n的最大值是(
) 上有n个不同的点:P1,P2,Pn,,椭圆的右焦点为F,数列{|PnF|}是公差大于
上有n个不同的点:P1,P2,Pn,,椭圆的右焦点为F,数列{|PnF|}是公差大于 的等差数列,则n的最大值为( )
的等差数列,则n的最大值为( )