题目内容
已知椭圆![]() 上有n个不同的点P1、P2、……、Pn, 其中点
上有n个不同的点P1、P2、……、Pn, 其中点![]() , 椭圆的右焦点为F, 记
, 椭圆的右焦点为F, 记![]() , 数列{an}构成以d为公差的等差数列,
, 数列{an}构成以d为公差的等差数列, ![]() .
.
(1)若![]() , 求点P3的坐标;
, 求点P3的坐标;
(2)若公差d为常数且![]() , 求n的最大值;
, 求n的最大值;
(3)对于给定的正整数![]() , 当公差d变化时, 求Sn的最大值.
, 当公差d变化时, 求Sn的最大值.
解析:对于椭圆![]() , 有
, 有![]() , 所以
, 所以![]() , 右准线
, 右准线![]()
设![]() , 于是由定义知
, 于是由定义知![]() , 即
, 即![]() …………………2分
…………………2分
(1)∵![]() , 所以
, 所以![]()
由![]()
![]() ,
,
∴![]()
故![]() ……………………4分
……………………4分
(2)由椭圆范围可知![]() , ∴
, ∴![]()
∵![]() 是等差数列,
是等差数列, ![]() 且
且![]()
∴![]() , ∴
, ∴![]() , 即
, 即![]() 的最大值为200……………………9分
的最大值为200……………………9分
(3)由(2)知, ![]() , ∴
, ∴![]() , ∴
, ∴![]()
由![]() , ∵
, ∵![]() , ∴
, ∴![]() 是关于
是关于![]() 的增函数
的增函数
∴![]() 的最大值为
的最大值为![]() ……………………14分
……………………14分

练习册系列答案
相关题目
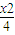 +
+ =1上有n个不同的点P1,P2,P3,…,Pn.设椭圆的右焦点为F,数列{|PnF|}是公差大于
=1上有n个不同的点P1,P2,P3,…,Pn.设椭圆的右焦点为F,数列{|PnF|}是公差大于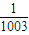 的等差数列,则n的最大值为( )
的等差数列,则n的最大值为( )