Question

【题目】已知椭圆C： （a＞b＞0）的左焦点为F（﹣2，0），离心率为 ． （Ⅰ）求椭圆C的标准方程；
（Ⅱ）设O为坐标原点，T为直线x=﹣3上一点，过F作TF的垂线交椭圆于P、Q，当四边形OPTQ是平行四边形时，求四边形OPTQ的面积．

Answer 1

【答案】解：（Ⅰ）由题意可得 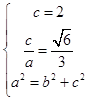， 解得c=2，a= ，b= ．
∴椭圆C的标准方程为 ；
（Ⅱ）由（Ⅰ）可得F（﹣2，0），
设T（﹣3，m），则直线TF的斜率 ，
∵TF⊥PQ，可得直线PQ的方程为x=my﹣2．
设P（x1 ， y1），Q（x2 ， y2）．
联立 ，化为（m2+3）y2﹣4my﹣2=0，
△＞0，∴y1+y2= ，y1y2= ．
∴x1+x2=m（y1+y2）﹣4= ．
∵四边形OPTQ是平行四边形，
∴ ，∴（x1 ， y1）=（﹣3﹣x2 ， m﹣y2），
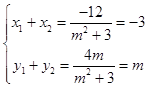∴ ，解得m=±1．
此时四边形OPTQ的面积S= ═ = ．
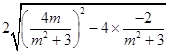【解析】（Ⅰ）由题意可得 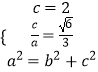，解出即可；（Ⅱ）由（Ⅰ）可得F（﹣2，0），设T（﹣3，m），可得直线TF的斜率kTF=﹣m，由于TF⊥PQ，可得直线PQ的方程为x=my﹣2．设P（x1 ， y1），Q（x2 ， y2）．直线方程与椭圆方程可得根与系数的关系．由于四边形OPTQ是平行四边形，可得 ，即可解得m．此时四边形OPTQ的面积S= ．