题目内容
甲、乙、丙三人参加某次招聘会,假设甲能被聘用的概率是 ,甲、丙两人同时不能被聘用的概率是
,甲、丙两人同时不能被聘用的概率是 ,乙、丙两人同时能被聘用的概率为
,乙、丙两人同时能被聘用的概率为 ,且三人各自能否被聘用相互独立.
,且三人各自能否被聘用相互独立.
(1)求乙、丙两人各自被聘用的概率;
(2)设 为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求
为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求 的分布列与均值(数学期望).
的分布列与均值(数学期望).
 ,甲、丙两人同时不能被聘用的概率是
,甲、丙两人同时不能被聘用的概率是 ,乙、丙两人同时能被聘用的概率为
,乙、丙两人同时能被聘用的概率为 ,且三人各自能否被聘用相互独立.
,且三人各自能否被聘用相互独立.(1)求乙、丙两人各自被聘用的概率;
(2)设
 为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求
为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求 的分布列与均值(数学期望).
的分布列与均值(数学期望).(1)乙、丙两人各自被聘用的概率分别为 、
、 ;(2)详见解析.
;(2)详见解析.
 、
、 ;(2)详见解析.
;(2)详见解析.试题分析:(1)分别设乙、丙两人各自被聘用的概率为
 、
、 ,利用事件的独立性列出相应的方程进行求解,从而得出乙、丙两人各自被聘用的概率;(2)先列举出随机变量
,利用事件的独立性列出相应的方程进行求解,从而得出乙、丙两人各自被聘用的概率;(2)先列举出随机变量 的可能取值,并根据事件的独立性求出
的可能取值,并根据事件的独立性求出 在相应条件的概率,列出分布列并求出随机变量
在相应条件的概率,列出分布列并求出随机变量 的均值(即数学期望).
的均值(即数学期望).试题解析:(1)设乙、丙两人各自被聘用的概率分别为
 、
、 ,
,则甲、丙两人同时不能被聘用的概率是
 ,解得
,解得 ,
,乙、丙两人同时能被聘用的概率为
 ,
,因此乙、丙两人各自被聘用的概率分别为
 、
、 ;
;(2)
 的可能取值有
的可能取值有 、
、 ,
,则

 ,
, ,
,因此随机变量
 的分布列如下表所示
的分布列如下表所示 |  |  |
 |  |  |
 的均值(即数学期望)
的均值(即数学期望) .
.
练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目

 名学生被考官L面试,求
名学生被考官L面试,求
 (
( ≥0)万元,投资B项目资金为
≥0)万元,投资B项目资金为 (
( ≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利
≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利 的可能性为
的可能性为 ,亏损
,亏损 的可能性为
的可能性为 ;位于二类风区的B项目获利
;位于二类风区的B项目获利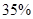 的可能性为
的可能性为 的可能性是
的可能性是 ,不赔不赚的可能性是
,不赔不赚的可能性是 .
. 和
和 ,试写出随机变量
,试写出随机变量 ,
, ;
; 万元的资金投资于A,B项目,且公司要求对A项目的投
万元的资金投资于A,B项目,且公司要求对A项目的投 的最大值.
的最大值. 为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求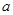 个红球,
个红球,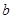 个黄球,
个黄球,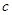 个蓝球,且规定:取出一个红球得1分,
个蓝球,且规定:取出一个红球得1分,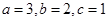 时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量
时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量 为取出此2球所得分数之和,.求
为取出此2球所得分数之和,.求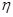 为取出此球所得分数.若
为取出此球所得分数.若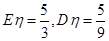 ,求
,求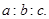
 ,P(ξ=n)=a.若E(ξ)=2,则D(ξ)的最小值等于 .
,P(ξ=n)=a.若E(ξ)=2,则D(ξ)的最小值等于 . 。
。 层楼,写出
层楼,写出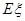 。
。