题目内容
设袋子中装有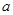 个红球,
个红球,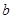 个黄球,
个黄球,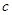 个蓝球,且规定:取出一个红球得1分,
个蓝球,且规定:取出一个红球得1分,
取出一个黄球2分,取出蓝球得3分。
(1)当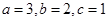 时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量
时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量 为取出此2球所得分数之和,.求
为取出此2球所得分数之和,.求 分布列;
分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量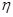 为取出此球所得分数.若
为取出此球所得分数.若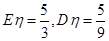 ,求
,求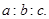
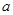 个红球,
个红球,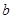 个黄球,
个黄球,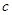 个蓝球,且规定:取出一个红球得1分,
个蓝球,且规定:取出一个红球得1分,取出一个黄球2分,取出蓝球得3分。
(1)当
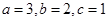 时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量
时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量 为取出此2球所得分数之和,.求
为取出此2球所得分数之和,.求 分布列;
分布列;(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量
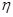 为取出此球所得分数.若
为取出此球所得分数.若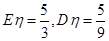 ,求
,求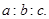
(1)
(2)3:2:1
 | 2 | 3 | 4 | 5 | 6 |
| P | 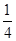 | 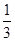 | 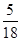 | 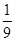 | 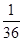 |
(2)3:2:1
此题关键是读懂题目的意思,即搞清楚游戏的规则,取球是有放回的且取出球的颜色不同得分也不相同,此题第(1)问如果不注意容易错误的理解为一次取出2个球;由题目的意思分析得到 的取值可能分别是2,3,4,5,6,即当两次摸到的球分别是红红时得2分,当两次摸到的球分别是红黄或黄红时得3分,当两次摸到的球分别是黄黄或红蓝或蓝红时得4分,当两次摸到的球分别是黄蓝或蓝黄时得5分,当两次摸到的球分别是蓝蓝时得6分;第(2)文关键是搞清楚随机变量
的取值可能分别是2,3,4,5,6,即当两次摸到的球分别是红红时得2分,当两次摸到的球分别是红黄或黄红时得3分,当两次摸到的球分别是黄黄或红蓝或蓝红时得4分,当两次摸到的球分别是黄蓝或蓝黄时得5分,当两次摸到的球分别是蓝蓝时得6分;第(2)文关键是搞清楚随机变量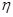 的取值有哪些,然后求出对应的概率,利用随机变量的期望和方差的计算公式列出关于
的取值有哪些,然后求出对应的概率,利用随机变量的期望和方差的计算公式列出关于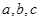 的方程即可求出他们关系;
的方程即可求出他们关系;
(1)由已知得到:当两次摸到的球分别是红红时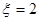 ,此时
,此时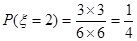 ;当两次摸到的球分别是黄黄,红蓝,蓝红时
;当两次摸到的球分别是黄黄,红蓝,蓝红时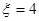 ,此时
,此时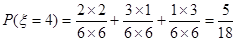 ;当两次摸到的球分别是红黄,黄红时
;当两次摸到的球分别是红黄,黄红时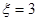 ,此时
,此时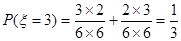 ;当两次摸到的球分别是黄蓝,蓝黄时
;当两次摸到的球分别是黄蓝,蓝黄时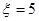 ,此时
,此时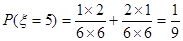 ;当两次摸到的球分别是蓝蓝时
;当两次摸到的球分别是蓝蓝时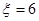 ,此时
,此时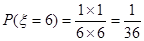 ;所以
;所以 的分布列是:
的分布列是:
(2)由已知得到: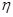 有三种取值即1,2,3,所以
有三种取值即1,2,3,所以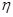 的分布列是:
的分布列是:
所以: ,所以
,所以
点评:此题考查概率与统计,考查离散型随机变量的分布列及期望和方差的计算;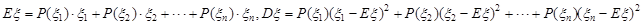 ;若服从正态分布,即
;若服从正态分布,即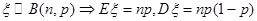 ;
;
 的取值可能分别是2,3,4,5,6,即当两次摸到的球分别是红红时得2分,当两次摸到的球分别是红黄或黄红时得3分,当两次摸到的球分别是黄黄或红蓝或蓝红时得4分,当两次摸到的球分别是黄蓝或蓝黄时得5分,当两次摸到的球分别是蓝蓝时得6分;第(2)文关键是搞清楚随机变量
的取值可能分别是2,3,4,5,6,即当两次摸到的球分别是红红时得2分,当两次摸到的球分别是红黄或黄红时得3分,当两次摸到的球分别是黄黄或红蓝或蓝红时得4分,当两次摸到的球分别是黄蓝或蓝黄时得5分,当两次摸到的球分别是蓝蓝时得6分;第(2)文关键是搞清楚随机变量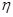 的取值有哪些,然后求出对应的概率,利用随机变量的期望和方差的计算公式列出关于
的取值有哪些,然后求出对应的概率,利用随机变量的期望和方差的计算公式列出关于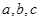 的方程即可求出他们关系;
的方程即可求出他们关系;(1)由已知得到:当两次摸到的球分别是红红时
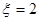 ,此时
,此时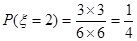 ;当两次摸到的球分别是黄黄,红蓝,蓝红时
;当两次摸到的球分别是黄黄,红蓝,蓝红时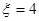 ,此时
,此时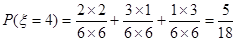 ;当两次摸到的球分别是红黄,黄红时
;当两次摸到的球分别是红黄,黄红时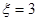 ,此时
,此时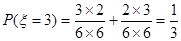 ;当两次摸到的球分别是黄蓝,蓝黄时
;当两次摸到的球分别是黄蓝,蓝黄时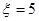 ,此时
,此时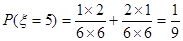 ;当两次摸到的球分别是蓝蓝时
;当两次摸到的球分别是蓝蓝时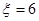 ,此时
,此时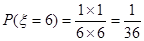 ;所以
;所以 的分布列是:
的分布列是: | 2 | 3 | 4 | 5 | 6 |
| P | 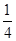 | 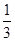 | 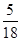 | 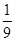 | 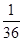 |
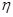 有三种取值即1,2,3,所以
有三种取值即1,2,3,所以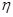 的分布列是:
的分布列是: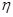 | 1 | 2 | 3 |
| P | 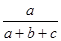 | 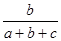 | 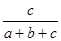 |
 ,所以
,所以
点评:此题考查概率与统计,考查离散型随机变量的分布列及期望和方差的计算;
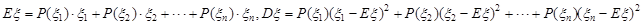 ;若服从正态分布,即
;若服从正态分布,即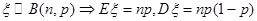 ;
;
练习册系列答案
相关题目

 ,甲、丙两人同时不能被聘用的概率是
,甲、丙两人同时不能被聘用的概率是 ,乙、丙两人同时能被聘用的概率为
,乙、丙两人同时能被聘用的概率为 ,且三人各自能否被聘用相互独立.
,且三人各自能否被聘用相互独立. 为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求
为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求 (i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?
(i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大? ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、 、p2.
、p2. ,落在圆盘中2分处的概率为
,落在圆盘中2分处的概率为 ,落在圆盘中0分处的概率为
,落在圆盘中0分处的概率为 ,(
,( ),已知旋转一次圆盘得分的数学期望为1分,则
),已知旋转一次圆盘得分的数学期望为1分,则 的最小值为
的最小值为



