题目内容
如图,旅客从某旅游区的景点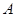 处下山至
处下山至 处有两种路径.一种是从
处有两种路径.一种是从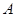 沿直线步行到
沿直线步行到 ,另一种从
,另一种从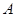 沿索道乘缆车到
沿索道乘缆车到 ,然后从
,然后从 沿直线步行到
沿直线步行到 .现有甲、乙两位游客从
.现有甲、乙两位游客从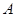 处下山,甲沿
处下山,甲沿 匀速步行,速度为
匀速步行,速度为 m/min,在甲出发2 min后,乙从
m/min,在甲出发2 min后,乙从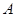 乘缆车到
乘缆车到 ,在
,在 处停留1 min后,再从
处停留1 min后,再从 匀速步行到
匀速步行到 . 假设缆车匀速直线运动的速度为130 m/min,山路
. 假设缆车匀速直线运动的速度为130 m/min,山路 长1260 m ,经测量,
长1260 m ,经测量, ,
, .
.

(1)求索道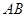 的长;
的长;
(2)问乙出发后多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
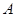 处下山至
处下山至 处有两种路径.一种是从
处有两种路径.一种是从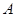 沿直线步行到
沿直线步行到 ,另一种从
,另一种从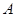 沿索道乘缆车到
沿索道乘缆车到 ,然后从
,然后从 沿直线步行到
沿直线步行到 .现有甲、乙两位游客从
.现有甲、乙两位游客从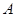 处下山,甲沿
处下山,甲沿 匀速步行,速度为
匀速步行,速度为 m/min,在甲出发2 min后,乙从
m/min,在甲出发2 min后,乙从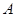 乘缆车到
乘缆车到 ,在
,在 处停留1 min后,再从
处停留1 min后,再从 匀速步行到
匀速步行到 . 假设缆车匀速直线运动的速度为130 m/min,山路
. 假设缆车匀速直线运动的速度为130 m/min,山路 长1260 m ,经测量,
长1260 m ,经测量, ,
, .
.
(1)求索道
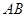 的长;
的长;(2)问乙出发后多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在
 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?(1) m (2)
m (2) (3)
(3) (单位:m/min)
(单位:m/min)
 m (2)
m (2) (3)
(3) (单位:m/min)
(单位:m/min)(1)在 中,∵
中,∵ ,
, ,∴
,∴ ,
, ,
,
从而 .
.
由正弦定理 ,得
,得 ,所以索道
,所以索道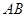 的长为1040(m).
的长为1040(m).
(2)假设乙出发 分钟后,甲、乙两游客距离为
分钟后,甲、乙两游客距离为 ,此时,甲行走了
,此时,甲行走了 m,乙距离
m,乙距离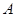 处
处 m,
m,
由余弦定理得 ,
,
∵ ,即
,即 ,故当
,故当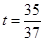 (min)时,甲、乙两游客距离最短.
(min)时,甲、乙两游客距离最短.
(3)由正弦定理, ,得
,得 (m),乙从
(m),乙从 出发时,甲走了
出发时,甲走了 (m),还需要走
(m),还需要走 (m)才能到达
(m)才能到达 ,
,
设乙步行的速度为 m/min,由题意,
m/min,由题意, ,解得
,解得 ,
,
∴为使两游客在 处互相等待的时间不超过3分钟,乙步行的速度应控制在
处互相等待的时间不超过3分钟,乙步行的速度应控制在 (单位:m/min)范围内.
(单位:m/min)范围内.
【考点定位】本小题主要考查正弦定理、余弦定理、二次函数的最值以及三角函数的基本关系、两角和的正弦等基础知识,考查数学阅读能力和分析解决实际问题的能力.
 中,∵
中,∵ ,
, ,∴
,∴ ,
, ,
,从而
 .
.由正弦定理
 ,得
,得 ,所以索道
,所以索道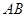 的长为1040(m).
的长为1040(m).(2)假设乙出发
 分钟后,甲、乙两游客距离为
分钟后,甲、乙两游客距离为 ,此时,甲行走了
,此时,甲行走了 m,乙距离
m,乙距离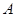 处
处 m,
m,由余弦定理得
 ,
,∵
 ,即
,即 ,故当
,故当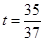 (min)时,甲、乙两游客距离最短.
(min)时,甲、乙两游客距离最短.(3)由正弦定理,
 ,得
,得 (m),乙从
(m),乙从 出发时,甲走了
出发时,甲走了 (m),还需要走
(m),还需要走 (m)才能到达
(m)才能到达 ,
,设乙步行的速度为
 m/min,由题意,
m/min,由题意, ,解得
,解得 ,
,∴为使两游客在
 处互相等待的时间不超过3分钟,乙步行的速度应控制在
处互相等待的时间不超过3分钟,乙步行的速度应控制在 (单位:m/min)范围内.
(单位:m/min)范围内.【考点定位】本小题主要考查正弦定理、余弦定理、二次函数的最值以及三角函数的基本关系、两角和的正弦等基础知识,考查数学阅读能力和分析解决实际问题的能力.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
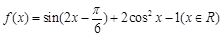 .
.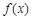 的单调递增区间;
的单调递增区间;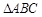 中,三内角
中,三内角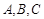 的对边分别为
的对边分别为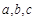 ,已知
,已知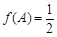 ,
,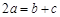 ,
,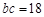 .求
.求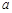 的值.
的值. ABC中,
ABC中, A
A ,
, ,则
,则 = .
= . ,求
,求 的取值范围.
的取值范围. 中,已知点
中,已知点 在
在 边上,
边上, ,
, ,
,  ,则
,则 的长为_____
的长为_____ 
 ,A=30°,则B等于 ( )
,A=30°,则B等于 ( ) ,则这个三角形的最大角为( )
,则这个三角形的最大角为( ) 121°,则此三角形解的情况是 。(填“无解”或“一解”或“两解”)
121°,则此三角形解的情况是 。(填“无解”或“一解”或“两解”)