题目内容
已知函数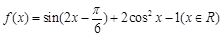 .
.
(1)求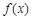 的单调递增区间;
的单调递增区间;
(2)在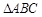 中,三内角
中,三内角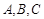 的对边分别为
的对边分别为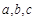 ,已知
,已知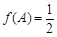 ,
,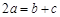 ,
,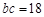 .求
.求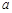 的值.
的值.
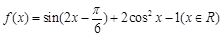 .
.(1)求
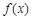 的单调递增区间;
的单调递增区间;(2)在
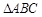 中,三内角
中,三内角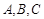 的对边分别为
的对边分别为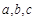 ,已知
,已知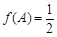 ,
,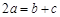 ,
,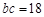 .求
.求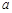 的值.
的值.(1)  ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)此类题目需将原函数化为一角一函数形式,然后根据正余弦函数的性质,确定单调区间;(2)先由
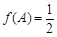 确定
确定 的值,然后利用余弦定理和条件解出
的值,然后利用余弦定理和条件解出 .
.试题解析:(1)

 3分
3分由
 得
得 5分
5分∴
 的单调递增区间为
的单调递增区间为 6分
6分(2)由
 得
得
∵
 ∴
∴ ∴
∴ 8分
8分由余弦定理得
 10分
10分又
 ∴
∴ 12分
12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的三个内角且向量
的三个内角且向量 与
与 共线.
共线. 的对边分别是
的对边分别是 ,且满足
,且满足 ,试判断
,试判断
 的形状.
的形状. ,
, ,
, 共线,其中
共线,其中 分别是
分别是 的三条边及相对三个角,则
的三条边及相对三个角,则 中,
中, ,
, ,
, ,则
,则



 中,
中, ,
, ,
, ,则
,则 .
.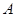 处下山至
处下山至 处有两种路径.一种是从
处有两种路径.一种是从 ,然后从
,然后从 匀速步行,速度为
匀速步行,速度为 m/min,在甲出发2 min后,乙从
m/min,在甲出发2 min后,乙从 ,
, .
.
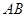 的长;
的长; 中,
中, ,则此三角形解的情况是 ( )
,则此三角形解的情况是 ( ) ,则函数
,则函数 的最大值是( )
的最大值是( )


 的三内角
的三内角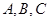 的对边分别为
的对边分别为 ,且满足
,且满足 ,则
,则