题目内容
已知 =(2sinx,1),
=(2sinx,1), =,其中m>0,若f(x)=
=,其中m>0,若f(x)= •
• ,且最大值
,且最大值 .
.(1)求m值.
(2)当
 时,求f(x)值域.
时,求f(x)值域.(3)直线3x-y+c=0是否可能和f(x)图象相切?叙述理由.
【答案】分析:(1)利用向量数量积公式,结合函数f(x)的最大值为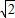 ,m>0,即可求得结论;
,m>0,即可求得结论;
(2)整体思维,求得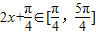 ,利用正弦函数的性质,可得结论;
,利用正弦函数的性质,可得结论;
(3)求导数,求得斜率的范围,可得结论.
解答:解:(1)∵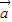 =(2sinx,1),
=(2sinx,1),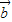 =(m•cosx-sinx,+1),
=(m•cosx-sinx,+1),
∴f(x)=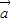 •
•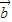 =msin2x-cos2x
=msin2x-cos2x
∵函数f(x)的最大值为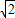 ,
,
∴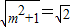
∴m=±1
∵m>0,∴m=1;
(2)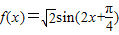 ,当
,当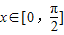 时,
时,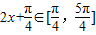
∴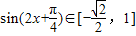
∴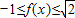 ,
,
∴函数f(x)的值域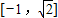 .
.
(3)3x-y+c=0不可能和f(x)图象相切.证明如下:
直线3x-y+c=0斜率k=3而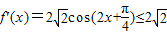
即f′(x)=3无解,故3x-y+c=0不可能和f(x)图象相切.
点评:本题考查向量的数量积公式,考查函数的值域,考查导数的几何意义,属于中档题.
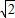 ,m>0,即可求得结论;
,m>0,即可求得结论;(2)整体思维,求得
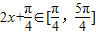 ,利用正弦函数的性质,可得结论;
,利用正弦函数的性质,可得结论;(3)求导数,求得斜率的范围,可得结论.
解答:解:(1)∵
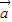 =(2sinx,1),
=(2sinx,1),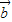 =(m•cosx-sinx,+1),
=(m•cosx-sinx,+1),∴f(x)=
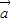 •
•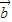 =msin2x-cos2x
=msin2x-cos2x∵函数f(x)的最大值为
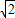 ,
,∴
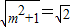
∴m=±1
∵m>0,∴m=1;
(2)
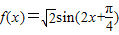 ,当
,当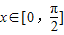 时,
时,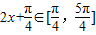
∴
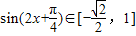
∴
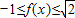 ,
,∴函数f(x)的值域
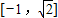 .
.(3)3x-y+c=0不可能和f(x)图象相切.证明如下:
直线3x-y+c=0斜率k=3而
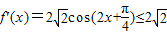
即f′(x)=3无解,故3x-y+c=0不可能和f(x)图象相切.
点评:本题考查向量的数量积公式,考查函数的值域,考查导数的几何意义,属于中档题.

练习册系列答案
相关题目