题目内容
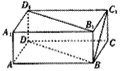（2012•西区模拟）如图，在长方体ABCD-A1B1C1D1中，AB=BC=2，AA1=1，则BC1与平面BDD1B1所成角的正弦值为
| ||
| 5 |
| ||
| 5 |
分析：连接A1C1交B1D1于O，连接BO，则可得∠C1BO为BC1与平面BBD1B1所成角，利用正弦函数，即可求得结论．
解答：
解：连接A1C1交B1D1于O，连接BO，则
∵长方体ABCD-A1B1C1D1中，AB=BC=2
∴C1O⊥平面BDD1B1
∴∠C1BO为BC1与平面BDD1B1所成角
∵C1O=
A1C1=
，BC1=
=
∴sin∠C1BO=
=
=
故答案为：
解：连接A1C1交B1D1于O，连接BO，则∵长方体ABCD-A1B1C1D1中，AB=BC=2
∴C1O⊥平面BDD1B1
∴∠C1BO为BC1与平面BDD1B1所成角
∵C1O=
| 1 |
| 2 |
| 2 |
| 4+1 |
| 5 |
∴sin∠C1BO=
| C1O |
| BC1 |
| ||
|
| ||
| 5 |
故答案为：
| ||
| 5 |
点评：本题考查线面角，解题的关键是正确作出线面角，属于中档题．
练习册系列答案
相关题目
（2012•西区模拟）如图，三棱锥P-ABC中，PA⊥平面ABC，PA=2，△ABC是边长为