题目内容
4.某几何体的三视图如图所示,则该几何体的体积为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | 1 | D. | 2 |
分析 根据三视图知几何体是三棱锥为棱长为2的正方体一部分,画出直观图,由三视图求出几何元素的长度,由锥体的体积公式求出几何体的体积.
解答 解:根据三视图知几何体是:
三棱锥P-ABC为长方体一部分,长、宽、高分别为2、2、1,
直观图如图所示:A、C分别是正方体的棱长的中点,
所以几何体的体积V=$\frac{1}{3}×\frac{1}{2}×1×1×1$=$\frac{1}{6}$
故选B.
点评 本题考查由三视图求几何体的条件,在三视图与直观图转化过程中,以一个长方体为载体是很好的方式,使得作图更直观,考查空间想象能力.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
12.设a=2ln$\frac{3}{2}$、b=log2$\frac{1}{3}$、c=($\frac{1}{2}$)-0.3,则( )
| A. | c<a<b | B. | a<c<b | C. | a<b<c | D. | b<a<c |
14.一个几何体的三视图如图所示,则这个几何体的表面积是( )
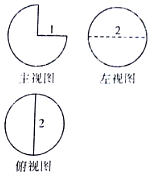

| A. | 3π | B. | 4π | C. | 5π | D. | $\frac{7π}{3}$ |
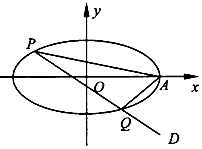 在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的焦距为2,离心率为$\frac{\sqrt{2}}{2}$,椭圆的右顶点为A.
在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的焦距为2,离心率为$\frac{\sqrt{2}}{2}$,椭圆的右顶点为A.