题目内容
设0<θ<π,则sin 的最大值为________.
的最大值为________.
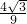
分析:可令y=sin
 (1+cosθ)=2
(1+cosθ)=2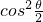 •sin
•sin ,则y2=2
,则y2=2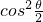 •
•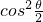 •2
•2 ≤2•
≤2• =
=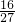 .开方即可.
.开方即可.解答:令y=sin
 (1+cosθ),则y=sin
(1+cosθ),则y=sin (1+cosθ)=2
(1+cosθ)=2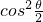 •sin
•sin ,
,∴y2=2
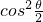 •
•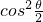 •(2
•(2 )≤2•
)≤2• =
=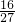 ,
,∴|y|≤
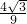 .
.故sin
 的最大值为
的最大值为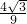 .
.点评:本题考查二倍角的余弦,难点在于解题突破口的思考:三个正数的基本不等式的应用,属于难题.

练习册系列答案
相关题目
设集合A={(x,y)|
},元素(3sinα,cos(
-α))∈A,0≤α<2π,则sinα的取值范围是( )
|
| π |
| 2 |
A、[-
| ||||
| B、[-1,1] | ||||
C、[-
| ||||
D、[-1,-
|
设0<α<β<
,sinα=
,cos(α-β)=
,则sinβ的值为( )
| π |
| 2 |
| 3 |
| 5 |
| 12 |
| 13 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若圆中一段弧长正好等于该圆外切正三角形的边长,设这段弧所对的圆心角是θ,则sinθ的值所在的区间为( )
A、(-
| ||||
B、(0,
| ||||
C、(
| ||||
D、(-1,-
|
 B.-
B.-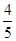 D.-
D.-