题目内容
18.函数f(x)=sin3x,满足$\frac{f({x}_{i})}{{x}_{i}}$=m,其中xi∈[-2π,2π],i=1,2,…n,n∈N*,则n的最大值为12.分析 由条件利用正弦函数的图象的特征,直线的斜率公式,求得n的最大值.
解答 解:函数f(x)=sin3x,满足$\frac{f({x}_{1})}{{x}_{1}}$=m,其中xi∈[-2π,2π],i=1,2,…n,n∈N*,
可得图象上的点(xi,f(x1))与原点连线的斜率为定值m,
故当n最大时,m=0,点(xi,f(xi))为f(x)的图象与x轴的交点(原点除外).
∵函数f(x)=sin3x的周期为$\frac{2π}{3}$,故[-2π,2π]包含6个周期,故满足$\frac{f({x}_{1})}{{x}_{1}}$=m的点(xi,f(xi))共有12个,
则n的最大值为12,
故答案为:12.
点评 本题主要考查正弦函数的图象的特征,直线的斜率公式,属于基础题.

练习册系列答案
相关题目
6.已知为虚数单位,复数z满足z=$\frac{1+i}{1-i}$,则z2=( )
| A. | 1 | B. | -1 | C. | 2i | D. | -2i |
13.复数z=$\frac{(1-i)^{2}}{3+i}$的所对应的点位于复平面的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.袋中装有5个同样大小的球,编号为1,2,3,4,5.现从该袋内随机取出3个球,记被取出的球的最大号码数为ξ,则Eξ等于( )
| A. | 4 | B. | 4.5 | C. | 4.75 | D. | 5 |
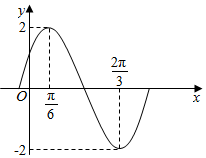 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)(x∈R)的部分图象如图所示.(Ⅰ)求函数f(x)的解析式并求函数f(x)的单调递增区间;
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)(x∈R)的部分图象如图所示.(Ⅰ)求函数f(x)的解析式并求函数f(x)的单调递增区间;