题目内容
已知函数f(x)=x|m-x|(x∈R),且f(4)=0.
(1)求实数m的值;
(2)作出函数f(x)的图象;
(3)根据图象写出不等式f(x)>0的解集
(4)求当x∈[1,5)时函数的值域.
(1)求实数m的值;
(2)作出函数f(x)的图象;
(3)根据图象写出不等式f(x)>0的解集
(4)求当x∈[1,5)时函数的值域.
考点:带绝对值的函数
专题:计算题,数形结合,函数的性质及应用
分析:(1)代入x=4,即可得到m;
(2)将f(x)写成分段函数的形式,画出函数的图象,注意自变量的范围;
(3)由图象观察x轴上方的自变量的范围,即可得到;
(4)观察x∈[1,5)时的图象,即可得到值域.
(2)将f(x)写成分段函数的形式,画出函数的图象,注意自变量的范围;
(3)由图象观察x轴上方的自变量的范围,即可得到;
(4)观察x∈[1,5)时的图象,即可得到值域.
解答:
 解:(1)函数f(x)=x|m-x|(x∈R),且f(4)=0,
解:(1)函数f(x)=x|m-x|(x∈R),且f(4)=0,
则f(4)=4|m-4|=0,即m=4.
(2)函数f(x)=x|x-4|=
,
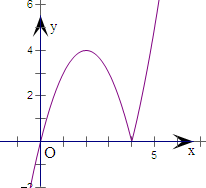
图象如图所示.
(3)由图象可得不等式f(x)>0的解集为:(0,4)∪(4,+∞).
(4)当x∈[1,5)时,f(1)=3,f(5)=5,f(4)=0,
则f(x)的值域为[0,5).
 解:(1)函数f(x)=x|m-x|(x∈R),且f(4)=0,
解:(1)函数f(x)=x|m-x|(x∈R),且f(4)=0,则f(4)=4|m-4|=0,即m=4.
(2)函数f(x)=x|x-4|=
|
图象如图所示.
(3)由图象可得不等式f(x)>0的解集为:(0,4)∪(4,+∞).
(4)当x∈[1,5)时,f(1)=3,f(5)=5,f(4)=0,
则f(x)的值域为[0,5).
点评:本题考查绝对值函数的图象和性质,考查数形结合的思想方法,考查通过图象解不等式和求函数的值域,属于中档题.

练习册系列答案
相关题目
数列{an}中,a1=2,an+1=an+cn(c是常数),且a1,a2,a3成公比不为1的等比数列,则a4=( )
| A、4 | B、8 | C、10 | D、14 |
函数y=
+
的定义域是( )
|
| 9-x |
A、(-
| ||
B、(-
| ||
C、[-
| ||
D、[-
|
函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
| A、(-1,+∞) |
| B、(-∞,-1) |
| C、(2,+∞) |
| D、(-∞,-2) |