题目内容
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=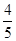 |PD|,当P在圆上运动时,求点M的轨迹C的方程。
|PD|,当P在圆上运动时,求点M的轨迹C的方程。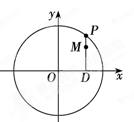

解析试题分析:这是一道典型的关于轨迹问题的题目,通常的解法:①设出所求轨迹点的坐标;②找出已知点的坐标与其之间的等量关系;③代入已知点的轨迹方程;④求出所求点的轨迹方程.在此题的解答过程中,可以先设出所求点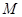 的坐标
的坐标 ,已知点
,已知点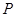 的坐标
的坐标 ,由“点
,由“点 是
是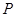 在
在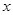 轴上的投影”且“
轴上的投影”且“ ”得到点
”得到点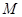 与点
与点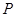 坐标之间的等量关系
坐标之间的等量关系 ,又由于点
,又由于点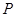 是已知圆上的点,将其坐标代入圆方程,经整理即可得到所点
是已知圆上的点,将其坐标代入圆方程,经整理即可得到所点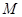 的轨迹方程.
的轨迹方程.
试题解析:设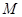 的坐标为
的坐标为 ,
,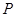 的坐标为
的坐标为 ,则由已知得
,则由已知得 5分
5分
因为点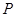 在圆上,所以
在圆上,所以 ,即所求点
,即所求点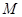 的轨迹
的轨迹 的方程为
的方程为 . 10分
. 10分
考点:轨迹问题

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
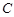 :
: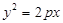 和⊙
和⊙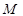 :
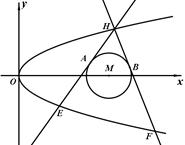
: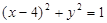 ,过抛物线
,过抛物线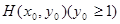 作两条直线与⊙
作两条直线与⊙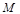 相切于
相切于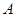 、
、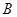 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点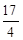 .
.
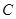 的方程;
的方程;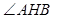 的角平分线垂直
的角平分线垂直 轴时,求直线
轴时,求直线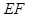 的斜率;
的斜率;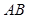 在
在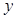 轴上的截距为
轴上的截距为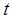 ,求
,求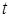 的最小值.
的最小值. 、
、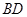 是过抛物线
是过抛物线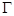 焦点
焦点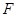 的两条弦,且其焦点
的两条弦,且其焦点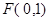 ,
,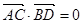 ,点
,点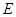 为
为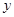 轴上一点,记
轴上一点,记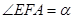 ,其中
,其中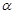 为锐角.
为锐角.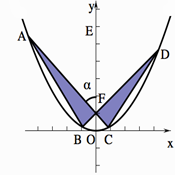
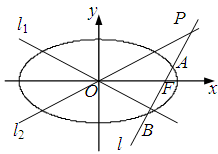
 的方程为
的方程为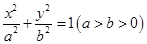 ,双曲线
,双曲线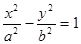 的两条渐近线为
的两条渐近线为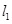 、
、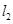 .过椭圆
.过椭圆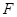 作直线
作直线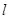 ,使
,使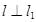 ,又
,又 交于点
交于点 ,设
,设 、
、 .
.
 与
与 ,且双曲线的焦距为
,且双曲线的焦距为 ,求椭圆
,求椭圆 的最大值.
的最大值.  的离心率为
的离心率为 ,其左焦点
,其左焦点 到点
到点 的距离为
的距离为 .
. 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点 、
、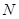 ,则
,则 内切圆的圆面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
内切圆的圆面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.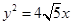 的焦点重合.
的焦点重合. 交椭圆C于A、B两点,试问在x轴上是否另存在一个定点P使得
交椭圆C于A、B两点,试问在x轴上是否另存在一个定点P使得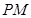 始终平分
始终平分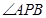 ?若存在求出
?若存在求出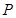 点坐标;若不存在请说明理由.
点坐标;若不存在请说明理由. (
(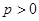 ,
,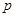 是常数),且动点
是常数),且动点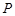 到
到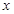 轴的距离比到点
轴的距离比到点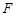 的距离小
的距离小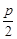 .
. 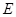 的方程;
的方程; ,若曲线
,若曲线 上存在不同两点
上存在不同两点 、
、 满足
满足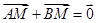 ,求实数
,求实数 时,抛物线
时,抛物线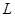 上是否存在异于
上是否存在异于 ,使得经过
,使得经过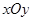 中,已知中心在原点,离心率为
中,已知中心在原点,离心率为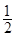 的椭圆E的一个焦点为圆
的椭圆E的一个焦点为圆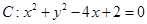 的圆心.
的圆心. ,当直线
,当直线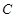 相切时,求P点坐标.
相切时,求P点坐标. :
: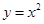 .过点
.过点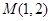 的直线
的直线 交
交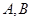 两点.抛物线
两点.抛物线 处的切线与在点
处的切线与在点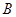 处的切线交于点
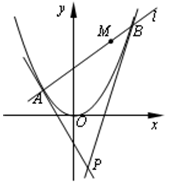
处的切线交于点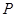 .
.
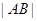 ;
;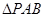 面积的最小值.
面积的最小值.