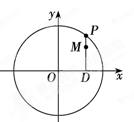
题目内容
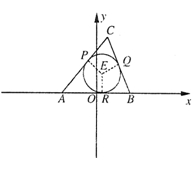
如图,已知抛物线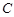 :
: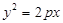 和⊙
和⊙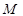 :
: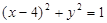 ,过抛物线
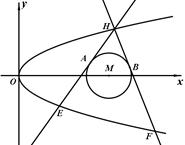
,过抛物线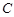 上一点
上一点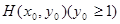 作两条直线与⊙
作两条直线与⊙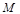 相切于
相切于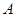 、
、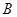 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点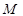 到抛物线准线的距离为
到抛物线准线的距离为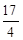 .
.
(1)求抛物线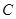 的方程;
的方程;
(2)当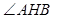 的角平分线垂直
的角平分线垂直 轴时,求直线
轴时,求直线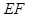 的斜率;
的斜率;
(3)若直线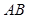 在
在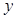 轴上的截距为
轴上的截距为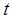 ,求
,求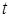 的最小值.
的最小值.
(1) ;(2)
;(2) ;(3)
;(3) ﹒
﹒
解析试题分析:(1)由题意知圆心 的坐标为
的坐标为 ,半径为1,抛物线
,半径为1,抛物线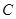 的准线方程为
的准线方程为 ,因为圆心
,因为圆心 到抛物线准线的距离为
到抛物线准线的距离为 ,所以有
,所以有 ,解得
,解得 ,从而求出抛物线方程为
,从而求出抛物线方程为 .
.
(2)由题意可知,直线 轴,可求出点
轴,可求出点 的坐标为
的坐标为 ,此时直线
,此时直线 与
与 的倾斜角互补,即
的倾斜角互补,即 ,又设点
,又设点 、
、 的坐标分别为
的坐标分别为 、
、 ,则
,则 ,
, ,所以有
,所以有 ,即
,即 ,整理得
,整理得 ,所以
,所以 .
.
(3)由题意可设点 、
、 的坐标分别为
的坐标分别为 、
、 ,则
,则 ,
, ,因为
,因为 、
、 是圆
是圆 的切线,所以
的切线,所以 、
、 ,因此
,因此 ,
, ,由点斜式可求出直线
,由点斜式可求出直线 、
、 的直线方程分别为
的直线方程分别为 、
、 ,又点
,又点 在抛物线上,有
在抛物线上,有 ,所以点
,所以点 的坐标为
的坐标为 ,代入直线
,代入直线 、
、 的方程得
的方程得 、
、 ,可整理为
,可整理为 、
、 ,从而可求得直线
,从而可求得直线 的方程为
的方程为 ,令
,令 ,得直线
,得直线 在
在 上的截距为
上的截距为 ,考虑到函数
,考虑到函数 为单调递增函数,所以
为单调递增函数,所以 .
.
试题解析:(1)∵点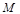 到抛物线准线的距离为
到抛物线准线的距离为
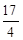 ,
,
∴ ,即抛物线
,即抛物线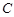 的方程为
的方程为 . 2分
. 2分
(2)法一:∵当 的角平分线垂直
的角平分线垂直 轴时,点
轴时,点 ,∴
,∴ ,
,
设 ,
, ,
,
∴ , ∴
, ∴  ,
,
∴ .&nbs
.&nbs

练习册系列答案
相关题目

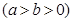 的离心率为
的离心率为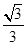 ,直线
,直线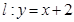 与圆
与圆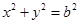 相切.
相切.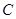 的方程;
的方程;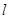 与椭圆
与椭圆 ,求弦长
,求弦长 .
.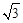 )和(0,
)和(0,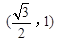 ,抛物线E的顶点在坐标原点,焦点F恰好是椭圆C的右顶点.
,抛物线E的顶点在坐标原点,焦点F恰好是椭圆C的右顶点.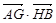 的最小值.
的最小值.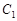 的极坐标方程为
的极坐标方程为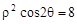 ,曲线
,曲线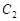 的极坐标方程为
的极坐标方程为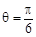 ,曲线
,曲线 、
、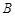 两点.(
两点.(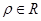 )
)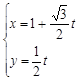 (
(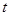 为参数)分别相交于
为参数)分别相交于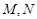 两点,求线段
两点,求线段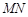 的长度.
的长度.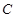 两焦点坐标分别为
两焦点坐标分别为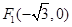 ,
,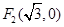 ,且经过点
,且经过点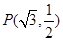 .
.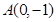 ,直线
,直线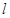 与椭圆
与椭圆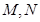 .若△
.若△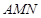 是以
是以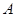 为直角顶点的等腰直角三角形,试求直线
为直角顶点的等腰直角三角形,试求直线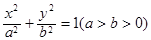 的左、右焦点分别为
的左、右焦点分别为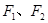 ,且
,且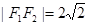 ,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.
,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.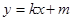 相交于不同的两点M、N,又点
相交于不同的两点M、N,又点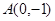 ,当
,当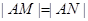 时,求实数m的取值范围,
时,求实数m的取值范围,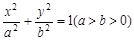 的左焦点,直线l:x=-
的左焦点,直线l:x=-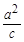 与x轴交于P点,MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|。
与x轴交于P点,MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|。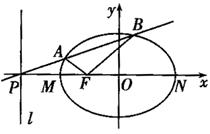
 的两顶点坐标
的两顶点坐标 ,
,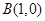 ,圆
,圆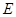 是
是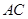 ,
,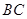 ,
, 上的切点分别为
上的切点分别为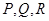 ,
,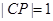 (从圆外一点到圆的两条切线段长相等),动点
(从圆外一点到圆的两条切线段长相等),动点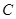 的轨迹为曲线
的轨迹为曲线 .
.
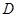 ,当点
,当点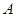 在以线段
在以线段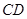 为直径的圆上时,求直线
为直径的圆上时,求直线 |PD|,当P在圆上运动时,求点M的轨迹C的方程。
|PD|,当P在圆上运动时,求点M的轨迹C的方程。