题目内容
某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中 、
、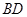 是过抛物线
是过抛物线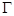 焦点
焦点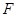 的两条弦,且其焦点
的两条弦,且其焦点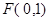 ,
,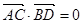 ,点
,点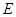 为
为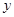 轴上一点,记
轴上一点,记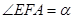 ,其中
,其中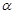 为锐角.
为锐角.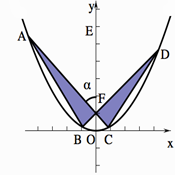
(1)求抛物线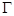 方程;
方程;
(2)如果使“蝴蝶形图案”的面积最小,求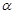 的大小?
的大小?
(1) ;(2)
;(2) .
.
解析试题分析:(1)抛物线焦点在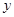 轴上,其标准方程为
轴上,其标准方程为 ,其中焦点坐标为
,其中焦点坐标为 ;(2)显然要把蝴蝶形图案”的面积表示为
;(2)显然要把蝴蝶形图案”的面积表示为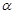 的函数,由于
的函数,由于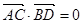 即
即 ,因此要求这个面积,只要求出
,因此要求这个面积,只要求出 的长,当然它们都要用
的长,当然它们都要用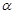 来表示,为此我们设
来表示,为此我们设 ,则
,则 点坐标为
点坐标为 ,利用点
,利用点 在抛物线
在抛物线 上,代入可得出关于
上,代入可得出关于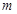 的二次方程,解方程求出
的二次方程,解方程求出 把
把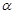 换成
换成 ,
, ,
, 可依次得到
可依次得到 ,由此我们就可把面积
,由此我们就可把面积 用
用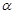 表示了,接下来只是涉及到求函数的最大值而已.
表示了,接下来只是涉及到求函数的最大值而已.
试题解析:(1)由抛物线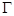 焦点
焦点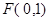 得,抛物线
得,抛物线 方程为
方程为
(2)设 ,则点
,则点
所以, ,既
,既

解得 
同理: 


“蝴蝶形图案”的面积
令 ,
, 
则 ,
,  时,即
时,即 “蝴蝶形图案”的面积为8.
“蝴蝶形图案”的面积为8.
考点:(1)抛物线的标准方程;(2)圆锥曲线综合问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 )和(0,
)和(0, ,抛物线E的顶点在坐标原点,焦点F恰好是椭圆C的右顶点.
,抛物线E的顶点在坐标原点,焦点F恰好是椭圆C的右顶点.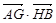 的最小值.
的最小值.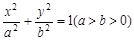 的左焦点,直线l:x=-
的左焦点,直线l:x=-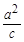 与x轴交于P点,MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|。
与x轴交于P点,MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|。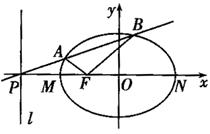
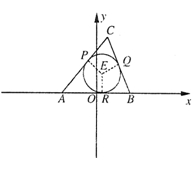
 的两顶点坐标
的两顶点坐标 ,
,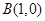 ,圆
,圆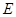 是
是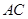 ,
,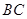 ,
, 上的切点分别为
上的切点分别为 ,
, (从圆外一点到圆的两条切线段长相等),动点
(从圆外一点到圆的两条切线段长相等),动点 的轨迹为曲线
的轨迹为曲线 .
.
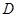 ,当点
,当点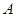 在以线段
在以线段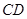 为直径的圆上时,求直线
为直径的圆上时,求直线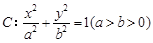 的离心率为
的离心率为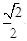 ,其中左焦点
,其中左焦点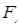 (-2,0).
(-2,0).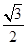 ,且经过点
,且经过点 ,直线
,直线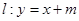 交椭圆于不同的两点A,B.
交椭圆于不同的两点A,B. 不过点M,求证:直线MA、MB与x轴围成一个等腰三角形
不过点M,求证:直线MA、MB与x轴围成一个等腰三角形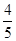 |PD|,当P在圆上运动时,求点M的轨迹C的方程。
|PD|,当P在圆上运动时,求点M的轨迹C的方程。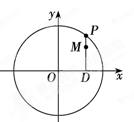
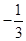 .
.