题目内容
12.已知数列{an}的通项公式an=nsin$\frac{nπ}{2}$,其前n项和为Sn,则S2016=-1008.分析 结合三角函数的周期性可知a4k-3=4k-3、a4k-2=0、a4k-1=-(4k-1)、a4k=0,进而可知a4k-3+a4k-2+a4k-1+a4k=-2,计算即得结论.
解答 解:因为an=nsin$\frac{nπ}{2}$,
所以a4k-3=4k-3,a4k-2=0,a4k-1=-(4k-1),a4k=0,
所以a4k-3+a4k-2+a4k-1+a4k=-2,
又因为504×4=2016,
所以S2016=504×(-2)=-1008,
故答案为:-1008.
点评 本题考查数列的求和,考查三角函数的周期性,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
17.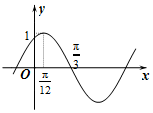 $f(x)=Asin(ωx+φ)(A>0,|φ|<\frac{π}{2})$的图象如图所示,为了得到f(x)的图象,则只要将g(x)=cos2x的图象( )
$f(x)=Asin(ωx+φ)(A>0,|φ|<\frac{π}{2})$的图象如图所示,为了得到f(x)的图象,则只要将g(x)=cos2x的图象( )
 $f(x)=Asin(ωx+φ)(A>0,|φ|<\frac{π}{2})$的图象如图所示,为了得到f(x)的图象,则只要将g(x)=cos2x的图象( )
$f(x)=Asin(ωx+φ)(A>0,|φ|<\frac{π}{2})$的图象如图所示,为了得到f(x)的图象,则只要将g(x)=cos2x的图象( )| A. | 向右平移$\frac{π}{12}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{12}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
2.与-30°终边相同的角是( )
| A. | -330° | B. | 150° | C. | 30° | D. | 330° |
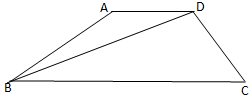 在四边形ABCD中,AD∥BC,AB=$\sqrt{3}$,AD=1,A=$\frac{5π}{6}$
在四边形ABCD中,AD∥BC,AB=$\sqrt{3}$,AD=1,A=$\frac{5π}{6}$