题目内容
4.给出下列命题:①若a<b<0,则$\frac{1}{a}$<$\frac{1}{b}$;②若a>0,b>0,则$\frac{a+b}{2}$≥$\sqrt{ab}$≥$\frac{ab}{a+b}$;③若a<b<0,则a2>ab>b2;④lg9•lg 11<1;⑤若a>b,$\frac{1}{a}$>$\frac{1}{b}$,则a>0,b<0;⑥正数x,y满足$\frac{1}{x}$+$\frac{1}{y}$=1,则x+2y的最小值为6.其中正确命题的序号是②③④⑤.分析 利用不等式的性质与基本不等式对①②③④⑤⑥逐项判断即可.
解答 解:①若a<b<0,则$\frac{1}{a}$>$\frac{1}{b}$,故①错误;
②若a>0,b>0,则$\frac{a+b}{2}$≥$\sqrt{ab}$(当且仅当a=b时取等号);
又$\sqrt{ab}$-$\frac{ab}{a+b}$=$\sqrt{ab}$(1-$\frac{\sqrt{ab}}{a+b}$)≥$\sqrt{ab}$(1-$\frac{\sqrt{ab}}{2\sqrt{ab}}$)=$\frac{1}{2}$$\sqrt{ab}$>0≥0,
所以$\sqrt{ab}$≥$\frac{ab}{a+b}$,综上,$\frac{a+b}{2}$≥$\sqrt{ab}$≥$\frac{ab}{a+b}$,故②正确;
③若a<b<0,则a2>ab>0,ab>b2>0,
因此,a2>ab>b2,故③正确;
④lg9•lg 11<($\frac{lg9+lg11}{2}$)2=${(\frac{lg99}{2})}^{2}$<${(\frac{lg100}{2})}^{2}$=1,故④正确;
⑤若a>b,$\frac{1}{a}$>$\frac{1}{b}$?$\frac{1}{a}$-$\frac{1}{b}$>0?$\frac{b-a}{ab}$>0?$\frac{a-b}{ab}$<0,则ab<0,所以a>0,b<0,故⑤正确;
⑥正数x,y满足$\frac{1}{x}$+$\frac{1}{y}$=1,则x+2y=(x+2y)($\frac{1}{x}$+$\frac{1}{y}$)=1+2+$\frac{2y}{x}$+$\frac{x}{y}$≥3+2$\sqrt{2}$,故其最小值为3+2$\sqrt{2}$,故⑥错误.
综上所述,正确命题的序号是:②③④⑤,
故答案为:②③④⑤.
点评 本题考查命题的真假判断与应用,突出考查不等式的性质与基本不等式的应用,属于中档题.

| x | 0 | 2 | 4 | 6 |
| y | a | 3 | 5 | 3a |
| A. | C${\;}_{8}^{4}$C${\;}_{4}^{2}$C${\;}_{2}^{2}$ | B. | C${\;}_{3}^{1}$C${\;}_{8}^{2}$ | ||
| C. | $\frac{{C}_{8}^{4}{C}_{4}^{2}}{{A}_{2}^{2}}$ | D. | $\frac{{C}_{8}^{4}{C}_{4}^{2}{C}_{2}^{2}}{{A}_{3}^{3}}$ |
| A. | $x+2y+\sqrt{5}=0$或$x+2y-\sqrt{5}=0$ | B. | $x-2y+\sqrt{5}=0$或$x-2y-\sqrt{5}=0$ | ||
| C. | x+2y+5=0或x+2y-5=0 | D. | x-2y+5=0或x-2y-5=0 |
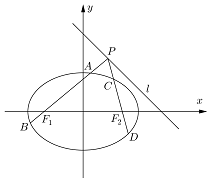 已知椭圆$M:\frac{x^2}{2}+{y^2}=1$左、右焦点分别为F1、F2,点p为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点;
已知椭圆$M:\frac{x^2}{2}+{y^2}=1$左、右焦点分别为F1、F2,点p为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点; 将全体正整数ai,j从左向右排成一个直角三角形数阵:
将全体正整数ai,j从左向右排成一个直角三角形数阵: