题目内容
若函数y=a1-x(a>0,a≠1)的图象过定点A,点A在直线mx+ny=1(m、n>0)上,则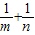 的最小值为( )
的最小值为( )A.5
B.2
C.7
D.4
【答案】分析:函数y=a1-x(a>0,a≠1)的图象恒过定点A,知A(1,1),点A在直线mx+ny-1=0上,得m+n=1结合mn>0,可得m>0,n>0,利用1的变换构造出可以用基本不等式求最值的形式求最值
解答:解:由已知定点A坐标为(1,1),由点A在直线mx+ny-1=0上,
∴m+n=1,
又mn>0,
∴m>0,n>0,
∴ =(
=( )(m+n)=2
)(m+n)=2

当且仅当 即m=n=
即m=n= 时取等号
时取等号
故选D
点评:本题主要考查了利用基本不等式求解最值,解题的关键是利用1的代换配凑基本不等式应用的条件
解答:解:由已知定点A坐标为(1,1),由点A在直线mx+ny-1=0上,
∴m+n=1,
又mn>0,
∴m>0,n>0,
∴
 =(
=( )(m+n)=2
)(m+n)=2

当且仅当
 即m=n=
即m=n= 时取等号
时取等号故选D
点评:本题主要考查了利用基本不等式求解最值,解题的关键是利用1的代换配凑基本不等式应用的条件

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
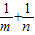 的最小值为( )
的最小值为( )