题目内容
过圆x2+y2=4上的一点(1,
)的圆的切线方程是 ( )
| 3 |
分析:求出圆心与已知点确定直线方程的斜率,利用两直线垂直时斜率的乘积为-1求出过此点切线方程的斜率,即可确定出切线方程.
解答:解:∵过(0,0)与(1,
)直线斜率为
,
∴过(1,
)切线方程的斜率为-
,
则所求切线方程为y-
=-
(x-1),即x+
y-4=0.
故选A
| 3 |
| 3 |
∴过(1,
| 3 |
| ||
| 3 |
则所求切线方程为y-
| 3 |
| ||
| 3 |
| 3 |
故选A
点评:此题考查了直线与圆的位置关系,涉及的知识有:两直线垂直时斜率满足的关系,以及直线的点斜式方程,找出切线方程的斜率是解本题的关键.

练习册系列答案
相关题目
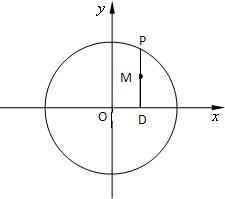 如图,P是圆x2+y2=4上的动点,P点在x轴上的投影是D,点M满足
如图,P是圆x2+y2=4上的动点,P点在x轴上的投影是D,点M满足