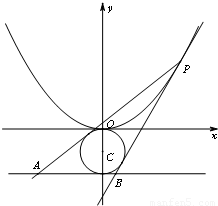
题目内容
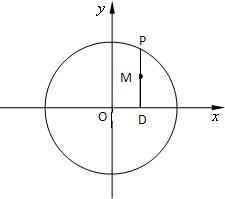 如图,P是圆x2+y2=4上的动点,P点在x轴上的投影是D,点M满足
如图,P是圆x2+y2=4上的动点,P点在x轴上的投影是D,点M满足| DM |
| 1 |
| 2 |
| DP |
(1)求动点M的轨迹C的方程,并说明轨迹是什么图形;
(2)过点N(3,0)的直线l与动点M的轨迹C交于不同的两点A,B,求以OA,OB为邻边的平行四边形OAEB的顶点E的轨迹方程.
(3)若存在点Q(a,0),使得四边形QAFB为菱形(A,B意义同(2)),求实数a的取值范围.
分析:(1)设点M(x,y),P(x0,y0),将其代入点M满足
=12
,用点M的坐标表示点P的坐标,代入圆x2+y2=4,化简即可求得动点M的轨迹C的方程,根据方程可知曲线的形状;
(2)设点E(x,y),A(x1,y1),B(x2,y2),根据题意设直线l的方程为y=k(x-3),联立方程,利用韦达定理,
=
+
,即可求得顶点E的轨迹方程;
(3)若存在点Q(a,0),使得四边形QAFB为菱形,可得QA=AB,代入,因式分解,利用韦达定理,用k表示a,转化为求函数的值域问题.
| DM |
| DP |
(2)设点E(x,y),A(x1,y1),B(x2,y2),根据题意设直线l的方程为y=k(x-3),联立方程,利用韦达定理,
| OE |
| OA |
| OB |
(3)若存在点Q(a,0),使得四边形QAFB为菱形,可得QA=AB,代入,因式分解,利用韦达定理,用k表示a,转化为求函数的值域问题.
解答:解:(1)设点M(x,y),P(x0,y0),
∵点M满足
=
.
∴x0=x,y0=2y
∵点P是圆x2+y2=4上的动点,
∴x2+4y2=4
即动点M的轨迹C的方程:
+y2=1,其图形为椭圆.
(2)设点E(x,y),A(x1,y1),B(x2,y2),根据题意设直线l的方程为y=k(x-3),
由
得(1+4k2)x2-24k2x+36k2-4=0
∵直线l与动点M的轨迹C交于不同的两点A,B,
∴△=(-24k2)2-4(1+4k2)(+36k2-4)>0,解得-
<k<
,
x1+x2=
,y1+y2=k(x1+x2-6)=
;
∵
=
+
,即
,
∴x=
,y=
,
∴顶点E的轨迹方程:x2+4y2-6x=0 (0<x<
).
(3)四边形QAFB为菱形,则QA=AB,即(x1-a)2+y12=(x2-a)2+y22,
∴k=
= -
=-
,
∴a=
=
,0<k2<
,解得0<a<1,
∴实数a的取值范围:(0,1).
∵点M满足
| DM |
| 1 |
| 2 |
| DP |
∴x0=x,y0=2y
∵点P是圆x2+y2=4上的动点,
∴x2+4y2=4
即动点M的轨迹C的方程:
| x2 |
| 4 |
(2)设点E(x,y),A(x1,y1),B(x2,y2),根据题意设直线l的方程为y=k(x-3),
由
|
∵直线l与动点M的轨迹C交于不同的两点A,B,
∴△=(-24k2)2-4(1+4k2)(+36k2-4)>0,解得-
| ||
| 5 |
| ||
| 5 |
x1+x2=
| 24k2 |
| 1+4k2 |
| -k |
| 1+4k2 |
∵
| OE |
| OA |
| OB |
|
∴x=
| 24k2 |
| 1+4k2 |
| -6k |
| 1+4k2 |
∴顶点E的轨迹方程:x2+4y2-6x=0 (0<x<
| 8 |
| 3 |
(3)四边形QAFB为菱形,则QA=AB,即(x1-a)2+y12=(x2-a)2+y22,
∴k=
| y2-y1 |
| x2-x1 |
| x1+x2-2a |
| y1+y2 |
| 24k2-2a(1+4k2) |
| -6k |
∴a=
| 18k2 |
| 2(1+4k2) |
| 9 | ||
4+
|
| 1 |
| 5 |
∴实数a的取值范围:(0,1).
点评:考查代入法求轨迹方程,以及直线与圆锥曲线的综合问题,这里侧重与几何图形的几何性质的考查,是把几何问题转化为代数问题的桥梁,综合性较强,特别是(3)的设问,把几何问题和函数的值域结合起来,增加了题目的难度,属难题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 已知抛物线x2=2py(p>0).抛物线上的点M(m,1)到焦点的距离为2
已知抛物线x2=2py(p>0).抛物线上的点M(m,1)到焦点的距离为2 (2012•浙江模拟)已知抛物线x2=4y.
(2012•浙江模拟)已知抛物线x2=4y. (2011•武昌区模拟)如图,已知点P是圆
(2011•武昌区模拟)如图,已知点P是圆