题目内容
已知等差数列{an}的前n项和为Sn.
(1)请写出数列{an}的前n项和Sn公式,并推导其公式;
(2)若an=n,数列{an}的前n项和为Sn,求
+
+…+
的和.
(1)请写出数列{an}的前n项和Sn公式,并推导其公式;
(2)若an=n,数列{an}的前n项和为Sn,求
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
考点:数列的求和,等差数列的前n项和
专题:等差数列与等比数列
分析:(1)等差数列的前n项和公式为Sn=
,利用倒序相加法进行证明.
(2)由已知条件推导出
=
=2(
-
),由此利用裂项求和法能求出
+
+…+
.
| n(a1+an) |
| 2 |
(2)由已知条件推导出
| 1 |
| Sn |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
解答:
解:(1)Sn=
或Sn=na1+
d.(注:只要写对其中一个公式即可)(2分)
证明:设等差数列{an}的公差为d,
∵Sn=a1+a2+…+an,…(3分)
∴Sn=a1+(a1+d)+(a1+2d)+…+[a1+(n-1)d],①…(4分)
Sn=an+(an-d)+(an-2d)+…+[an-(n-1)d],②…(5分)
由①+②得:2Sn=
…(6分)
=n(a1+an).…(7分)
所以Sn=
.…(8分)
(注:由于推导等差数列前n项和Sn公式的方法比较多,其它方法按相应的步骤给分)
(2)∵an=n,∴a1=1,Sn=1+2+…+n=
,…(9分)
∴
=
=2(
-
),…(10分)
∴
+
+…+
=2[(1-
)+(
-
)+…+(
-
)]…(11分)
=2(1-
)
=
.…(12分)
| n(a1+an) |
| 2 |
| n(n-1) |
| 2 |
证明:设等差数列{an}的公差为d,
∵Sn=a1+a2+…+an,…(3分)
∴Sn=a1+(a1+d)+(a1+2d)+…+[a1+(n-1)d],①…(4分)
Sn=an+(an-d)+(an-2d)+…+[an-(n-1)d],②…(5分)
由①+②得:2Sn=
| ||
| n个(a1+an) |
=n(a1+an).…(7分)
所以Sn=
| n(a1+an) |
| 2 |
(注:由于推导等差数列前n项和Sn公式的方法比较多,其它方法按相应的步骤给分)
(2)∵an=n,∴a1=1,Sn=1+2+…+n=
| n(n+1) |
| 2 |
∴
| 1 |
| Sn |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
=2[(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=2(1-
| 1 |
| n+1 |
=
| 2n |
| n+1 |
点评:本题考查等差数列前n项和的证明,考查数列的前n项和的求法,解题时要注意倒序相加法和裂项求和法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法中,正确的是( )
| A、命题“存在x∈R,x2-x>0”的否定是“对任意x∈R,x2-x<0”. |
| B、设α,β为两个不同的平面,直线l?α,则“l⊥β”是“α⊥β”成立的必要不充分条件. |
| C、命题“若a<b,则am2<bm2”的否命题是真命题. |
| D、已知x∈R,则“x>1”是“x>2”的充分不必要条件. |
某中学进行模拟考试有80个考室,每个考室30个考生,每个考试座位号按1~30号随机抽取试卷进行评分标准,每个考场抽取座位号为15号考生试卷质检,这种抽样方法是( )
| A、简单随机抽样 | B、系统抽样 |
| C、分层抽样 | D、分组抽样 |
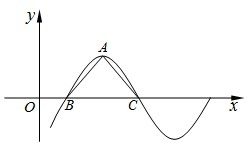 已知函数
已知函数