Question

【题目】设抛物线的焦点为，过点的动直线交抛物线于不同两点，线段中点为，射线与抛物线交于点.

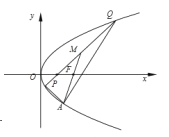
（1）求点的轨迹方程；

（2）求面积的最小值.

Answer 1

【答案】（1）；（2）

【解析】分析：（1）设直线方程为，代入，消去，运用韦达定理和中点坐标公式，再运用代入法消去，即可得到的轨迹方程；（2）设，根据（1）可得，由点在抛物线上，化简可得，由点到直线的距离公式，以及弦长公式，求出的面积，再构造新函数，利用导数即可求得的面积的最小值.

详解：（1）设直线方程为，代入得

设，则， ， .

∴.

设，由消去得中点的轨迹方程为

（2）设.

∵，

∴

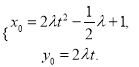
由点在抛物线上，得.

又∵

∴，点到直线的距离

又 .

所以， 面积

设，有，故在上是减函数，在上是增函数，因此，当时取到最小值.

所以， 面积的最小值是.