题目内容
已知f(x)=3x2-x+m,(x∈R),g(x)=lnx(1)若函数 f(x)与 g(x)的图象在 x=x处的切线平行,求x的值;
(2)求当曲线y=f(x)与y=g(x)有公共切线时,实数m的取值范围;并求此时函数F(x)=f(x)-g(x)在区间
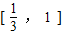 上的最值(用m表示).
上的最值(用m表示).
【答案】分析:(1)先求出f(x)和g(x)的导数,根据函数 f(x)与 g(x)的图象在 x=x处的切线平行,可知斜率相等,也即f′(x)和g′(x)在x=x处的值相等,从而求出x的值,同时注意由于g(x)=lnx,可知x>0判断x的取值;
(2)由题知曲线y=f(x)与y=g(x)有公共切线时,说明有公共切点,根据(1)可知切点横坐标为 ,可以求出m的范围,已知函数F(x)=f(x)-g(x),代入进行求导,令F′(x)=0,求出极值点,判断单调区间,列表求其最值;
,可以求出m的范围,已知函数F(x)=f(x)-g(x),代入进行求导,令F′(x)=0,求出极值点,判断单调区间,列表求其最值;
解答: 解:(1)∵f′(x)=6x-1,
解:(1)∵f′(x)=6x-1,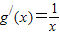 …(2分)
…(2分)
由题意知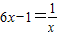 ,即
,即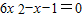 …(3分)
…(3分)
解得,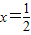 或
或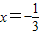 …(4分)
…(4分)
∵x>0,∴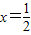 …(5分)
…(5分)
(2)若曲线y=f(x)与y=g(x)相切且在交点处有公共切线
由(1)得切点横坐标为 ,…(6分)
,…(6分)
∴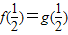 ,
,
∴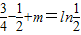 ,
,
∴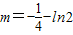 ,…(8分)
,…(8分)
由数形结合可知,当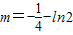 时,f(x)与g(x)有公共切线 …(9分)
时,f(x)与g(x)有公共切线 …(9分)
∵函数F(x)=f(x)-g(x),
∴F'(x)=f′(x)-g′(x)=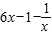 =
=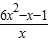 =
=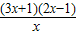 …(10分)
…(10分)
则F'(x)与F(x)在区间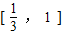 的变化如下表:
的变化如下表:
…(12分)
又∵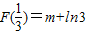 ,
,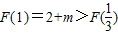
∴当x∈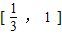 时,
时,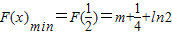 ,(
,(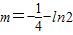 ),
),
F(x)max=F(1)=m+2,(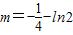 ) …(14分)
) …(14分)
点评:第一问容易出错的是x>0的隐含条件,许多同学不知道,从而得出两个x的值;第二问对F(x)正确求导,并求出极值是解题的关键,对这类利用导数求函数最值问题,用列表的方式来求解,不会容易出错,本题难度不大;
(2)由题知曲线y=f(x)与y=g(x)有公共切线时,说明有公共切点,根据(1)可知切点横坐标为
 ,可以求出m的范围,已知函数F(x)=f(x)-g(x),代入进行求导,令F′(x)=0,求出极值点,判断单调区间,列表求其最值;
,可以求出m的范围,已知函数F(x)=f(x)-g(x),代入进行求导,令F′(x)=0,求出极值点,判断单调区间,列表求其最值;解答:
 解:(1)∵f′(x)=6x-1,
解:(1)∵f′(x)=6x-1,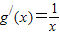 …(2分)
…(2分)由题意知
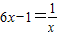 ,即
,即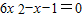 …(3分)
…(3分)解得,
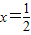 或
或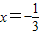 …(4分)
…(4分)∵x>0,∴
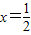 …(5分)
…(5分)(2)若曲线y=f(x)与y=g(x)相切且在交点处有公共切线
由(1)得切点横坐标为
 ,…(6分)
,…(6分)∴
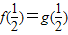 ,
,∴
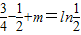 ,
,∴
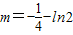 ,…(8分)
,…(8分)由数形结合可知,当
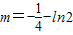 时,f(x)与g(x)有公共切线 …(9分)
时,f(x)与g(x)有公共切线 …(9分)∵函数F(x)=f(x)-g(x),
∴F'(x)=f′(x)-g′(x)=
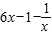 =
=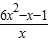 =
=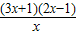 …(10分)
…(10分)则F'(x)与F(x)在区间
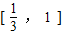 的变化如下表:
的变化如下表:| x | 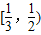 |  | 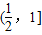 |
| F'(x) | - | + | |
| F(x) | ↘ | 极小值 | ↗ |
又∵
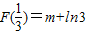 ,
,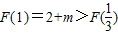
∴当x∈
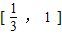 时,
时,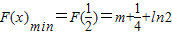 ,(
,(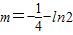 ),
),F(x)max=F(1)=m+2,(
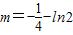 ) …(14分)
) …(14分)点评:第一问容易出错的是x>0的隐含条件,许多同学不知道,从而得出两个x的值;第二问对F(x)正确求导,并求出极值是解题的关键,对这类利用导数求函数最值问题,用列表的方式来求解,不会容易出错,本题难度不大;

练习册系列答案
相关题目