题目内容
【题目】已知函数f(x)=(ax-2)ex在x=1处取得极值.
(1)求a的值;
(2)求函数在区间[m,m+1]上的最小值.
【答案】(1)1(2)f(x)min=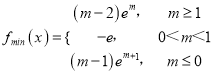 .
.
【解析】
(1)f′(x)=aex+(ax﹣2)ex=(ax+a﹣2)ex,由此利用导数性质能求出a=1.
(2)由f(x)=(x﹣2)ex,得f′(x)=ex+(x﹣2)ex=(x﹣1)ex.由f′(x)=0,得x=1,由此列表讨论,能求出f(x)在[m,m+1]上的最小值.
解 (1)f′(x)=(ax+a-2)ex,
由已知得f′(1)=(a+a-2)e=0,
解得a=1,经检验a=1符合题意,
所以a的值为1.
(2)由(1)得f(x)=(x-2)ex,f′(x)=(x-1)ex.
令f′(x)>0得x>1,令f′(x)<0得x<1.
所以函数f(x)在(-∞,1)上递减,在(1,+∞)上递增.
当m≥1时,f(x)在[m,m+1]上递增,f(x)min=f(m)=(m-2)em,
当0<m<1时,f(x)在[m,1]上递减,在(1,m+1]上递增,f(x)min=f(1)=-e.
当m≤0时,m+1≤1,f(x)在[m,m+1]上单调递减,
f(x)min=f(m+1)=(m-1)em+1.
综上,f(x)在[m,m+1]上的最小值为
f(x)min=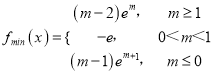 .
.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
【题目】某地区随着经济的发展,居民收入逐年增长,银行储蓄连年增长,下表是该地区某银行连续五年的储蓄存款(年底结算):
年份 |
|
|
|
|
|
储蓄存款 |
|
|
|
|
|
为方便研究,工作人员对上表的数据做了如下处理:![]() ,
,![]() 得到下表:
得到下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)通过(1)中的方程,求出![]() 关于
关于![]() 的线性回归方程,并用所求回归方程预测
的线性回归方程,并用所求回归方程预测![]() 年底,该地储蓄存款额可达多少?
年底,该地储蓄存款额可达多少?
(附:参考公式![]() ,其中
,其中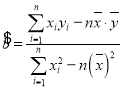 ,
,![]() )
)