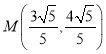题目内容
【题目】已知圆![]() ,圆
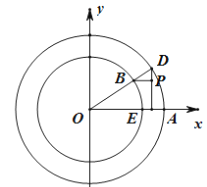
,圆![]() ,如图,C1,C2分别交x轴正半轴于点E,A.射线OD分别交C1,C2于点B,D,动点P满足直线BP与y轴垂直,直线DP与x轴垂直.
,如图,C1,C2分别交x轴正半轴于点E,A.射线OD分别交C1,C2于点B,D,动点P满足直线BP与y轴垂直,直线DP与x轴垂直.
(1)求动点P的轨迹C的方程;
(2)过点E作直线l交曲线C与点M,N,射线OH⊥l与点H,且交曲线C于点Q.问:![]() 的值是否是定值?如果是定值,请求出该定值;如果不是定值,请说明理由.
的值是否是定值?如果是定值,请求出该定值;如果不是定值,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 为定值,且为
为定值,且为![]() .
.
【解析】
(1)设![]() ,根据圆的方程求出
,根据圆的方程求出![]() 的坐标,进而可得
的坐标,进而可得![]() ,
,![]() ,然后得出动点P的轨迹C的方程.
,然后得出动点P的轨迹C的方程.
(2)设出直线l的方程为![]() ,联立直线与椭圆的方程,利用韦达定理,结合弦长公式,转化求解即可.
,联立直线与椭圆的方程,利用韦达定理,结合弦长公式,转化求解即可.
(1)设![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以动点![]() 的轨迹C的方程为
的轨迹C的方程为![]() .
.
(2)由(1)可知E为C的焦点,设直线l的方程为![]() (斜率不为0时),
(斜率不为0时),

且设点M(x1,y1),N(x2,y2),由 ,
,
得![]() ,
,
所以 ,所以
,所以 ,
,
又射线OQ方程为y=﹣mx,代入椭圆C的方程得x2+2(my)2=4,
即![]() ,
,![]()
 ,所以
,所以 ,
,
又当直线l的斜率为0时,也符合条件.
综上,![]() 为定值,且为
为定值,且为![]() .
.

练习册系列答案
相关题目