题目内容
4.已知命题“如果-1≤a≤1,那么关于x的不等式(a2-4)x2+(a+2)x-1≥0的解集为∅”,它的逆命题、否命题、逆否命题及原命题中是假命题的共有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 4个 |
分析 根据四种命题之间的关系利用逆否命题的真假关系进行判断即可.
解答 解:若不等式(a2-4)x2+(a+2)x-1≥0的解集为∅”,
则根据题意需分两种情况:
①当a2-4=0时,即a=±2,
若a=2时,原不等式为4x-1≥0,解得x≥$\frac{1}{4}$,故舍去,
若a=-2时,原不等式为-1≥0,无解,符合题意;
②当a2-4≠0时,即a≠±2,
∵(a2-4)x2+(a+2)x-1≥0的解集是空集,
∴$\left\{\begin{array}{l}{{a}^{2}-4<0}\\{△=(a+2)^{2}-4{(a}^{2}-4)×(-1)<0}\end{array}\right.$,解得$-2<a<\frac{6}{5}$,
综上得,实数a的取值范围是$[-2,\frac{6}{5})$.
则当-1≤a≤1时,命题为真命题,则命题的逆否命题为真命题,
反之不成立,即逆命题为假命题,否命题也为假命题,
故它的逆命题、否命题、逆否命题及原命题中是假命题的共有2个,
故选:C.
点评 本题考查了二次不等式的解法,四种命题真假关系的应用,注意当二次项的系数含有参数时,必须进行讨论,考查了分类讨论思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.用最小二乘法计算利润额y对销售额x的回归直线方程,当销售额为4(千万元)时,估计利润额的大小( )
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
| A. | 2.3 | B. | 3.2 | C. | 4.2 | D. | 2.4 |
13.已知集合A={x|x2-2x≤0},B={-1,0,1},则A∩B=( )
| A. | {-1} | B. | {0} | C. | {0,1} | D. | {1} |

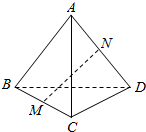 如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为30°或60°.
如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为30°或60°.