题目内容
8.已知数集A={a1,a2,a3,a4,a5}(0≤a1<a2<a3<a4<a5)具有性质p:对任意i,j∈Z,其中1≤i≤j≤5,aj+ai与aj-ai两数中至少有一个属于A,若a5=60,则a1=0,a3=30.分析 对a1分类讨论,利用性质p:对任意i,j∈Z,其中1≤i≤j≤5,均有(aj-ai)∈A,及其a5=60,即可得出答案.
解答 解:∵对任意i,j∈Z,其中1≤i≤j≤5,均有aj+ai与aj-ai两数中至少有一个属于A,
∵i=j=5时,aj+ai∉A,
∴aj-ai=0∈A,
∴a1=0;
a1=0,
∵i=4,j=5时,aj+ai∉A,
∴aj-ai∈A,
故a2=a5-a4,
∵i=3,j=5时,aj+ai∉A,
∴aj-ai∈A,
故a3=a5-a3,
∴a3=30,
故答案为:0,30
点评 本题考查了满足某种性质的数列、集合的求法,考查了分类讨论思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
3.已知am=-2,则a2m的值为( )
| A. | -4 | B. | 4 | C. | (-2)m | D. | 2m |
13.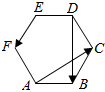 如图,正六边形ABCDEF中,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,则$\overrightarrow{EF}$等于( )
如图,正六边形ABCDEF中,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,则$\overrightarrow{EF}$等于( )
 如图,正六边形ABCDEF中,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,则$\overrightarrow{EF}$等于( )
如图,正六边形ABCDEF中,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,则$\overrightarrow{EF}$等于( )| A. | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ | B. | $\frac{1}{4}$$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$ | C. | $\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{1}{3}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{a}$ |
20.函数y=($\frac{1}{2}$)x-log2x的零点为x0,则( )
| A. | x0<1 | B. | x0>3 | C. | 2<x0<3 | D. | 1<x0<2 |