题目内容
7．已知y=f（x）是定义在R上的偶函数，在区间[0，+∞）上单调递增，且f（1）=0，那么不等式$\frac{f（x）}{x}$＞0的解集是（ ）| A． | {x|x＞1或-1＜x＜0} | B． | {x|x＞1或x＜-1} | C． | {x|0＜x＜1或x＜-1} | D． | {x|-1＜x＜1且x≠0} |
分析 根据函数的奇偶性和单调性之间的关系，将不等式进行转化，即可得到不等式的解集．
解答 
解：∵偶函数f（x）在[0，+∞）上为增函数，f（1）=0，
∴对应的图象如图：
不等式$\frac{f（x）}{x}$＞0等价为$\left\{\begin{array}{l}{x＞0}\\{f（x）＞0}\end{array}\right.$或$\left\{\begin{array}{l}{x＜0}\\{f（x）＜0}\end{array}\right.$，
即-1＜x＜0或x＞1，
即不等式的解集为{x|x＞1或-1＜x＜0}，
故选：A．
点评 本题主要考查不等式的解法，利用函数的奇偶性和单调性之间的关系是解决本题的关键，综合考查函数性质的应用．
练习册系列答案
阅读快车系列答案
相关题目
15．函数f（x）=x2在区间[$\frac{i-1}{n}$，$\frac{i}{n}$]上（ ）
| A． | 函数f（x）的值变化很小 | B． | 函数f（x）的值变化很大 | ||
| C． | 函数f（x）的值不变化 | D． | 当n很大时，函数f（x）的值变化很小 |
15．已知函数$f（x）=\left\{\begin{array}{l}{x^2}+2x，x∈（-∞，0）\\ ln（x+1），x∈[0，+∞）.\end{array}\right.g（x）={x^2}-4x-4$，若存在实数a，使得f（a）+g（x）=0，则x的取值范围为（ ）
| A． | [-1，5] | B． | （-∞，-1]∪[5，+∞） | C． | [-1，+∞） | D． | （-∞，5] |
2．已知角α的顶点与直角坐标系的原点重合，始边与x轴的非负半轴重合，若点P（1，-$\sqrt{3}$）是角α终边上一点，则tanα的值为（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{\sqrt{3}}{2}$ | C． | -$\sqrt{3}$ | D． | -$\frac{\sqrt{3}}{2}$ |
12．已知a＞0，函数f（x）=$\frac{|x-2a|}{x+2a}$在区间[1，4]上的最大值等于$\frac{1}{2}$，则a的值为（ ）
| A． | $\frac{2}{3}$或$\frac{3}{2}$ | B． | $\frac{3}{2}$ | C． | 2 | D． | $\frac{3}{2}$或2 |
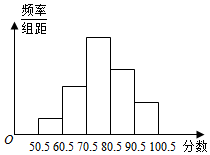从全校参加信息技术知识竞赛学生的试卷中，抽取一个样本，考察竞赛的成绩分布，将样本分成5组，绘成频率分布直方图，图中从左到右各小组的长方形的高之比是1：3：6：4：2，最中间一组的频数是18，请结合直方图提供的信息，解答下列问题：