题目内容
7.若“m≤a”是“方程x2+x+m=0有实数根”的充分条件,则实数a的取值范围是a≤$\frac{1}{4}$.分析 先求出方程x2+x+m=0有实数根成立的充要条件,从而判断出a的范围即可.
解答 解:若方程x2+x+m=0有实数根,
则△=1-4m≥0,解得:m≤$\frac{1}{4}$,
若“m≤a”是“方程x2+x+m=0有实数根”的充分条件,
则实数a的取值范围是:$a≤\frac{1}{4}$;
故答案为:a≤$\frac{1}{4}$.
点评 本题考查了充分必要条件,考查方程的根的情况,是一道基础题.

练习册系列答案
相关题目
15.函数y=lg(4-2x)的定义域是( )
| A. | (2,4) | B. | (2,+∞) | C. | (0,2) | D. | (-∞,2) |
12.设命题p:?x>1,x2-x+1>0,则?p为( )
| A. | ?x≤1,x2-x+1≤0 | B. | ?x>1,x2-x+1≤0 | C. | ?x>1,x2-x+1≤0 | D. | ?x≤1,x2-x+1>0 |
19.已知函数y=f(x+1)的图象过点(3,2),则函数y=-f(x)的图象一定过点( )
| A. | (2,-2) | B. | (2,2) | C. | (-4,2) | D. | (4,-2) |
16.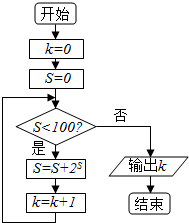 如果执行如图所示的程序,那么输出的值k=( )
如果执行如图所示的程序,那么输出的值k=( )
 如果执行如图所示的程序,那么输出的值k=( )
如果执行如图所示的程序,那么输出的值k=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |