题目内容
15．试求以点（3，3）为圆心，并与圆x2+y2=1相切的圆的方程．分析 利用圆心距等于半径和与差，求出所求圆的半径，即可得到所求圆的标准方程．
解答 解：设所求圆的半径为r，
由题意可知：$\sqrt{{3}^{2}+{3}^{2}}=3\sqrt{2}$=r+1，或$\sqrt{{3}^{2}+{3}^{2}}=3\sqrt{2}$=r-1，
解得r=$3\sqrt{2}-1$或$3\sqrt{2}+1$，
∴所求圆的方程为：（x-3）2+（y-3）2=19-$6\sqrt{2}$或（x-3）2+（y-3）2=19+$6\sqrt{2}$．
点评 本题考查圆与圆的位置关系，两点间的距离的求法，考查计算能力，是基础题．
练习册系列答案
相关题目
6．设函数f（x）=x-2sinx是区间[t，t+$\frac{π}{2}$]上的减函数，则实数t的取值范围是（ ）
| A． | [2kπ$-\frac{π}{3}$，2kπ$-\frac{π}{6}$]（k∈Z） | B． | [2kπ$+\frac{π}{3}$，2kπ$+\frac{11π}{6}$]（k∈Z） | ||
| C． | [2kπ$-\frac{π}{6}$，2kπ$+\frac{π}{3}$]（k∈Z） | D． | [2kπ$+\frac{π}{3}$，2kπ$+\frac{7π}{6}$]（k∈Z） |
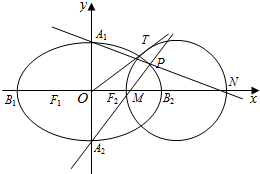已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率$e=\frac{{\sqrt{3}}}{2}$，椭圆C的上、下顶点分别为A1，A2，左、右顶点分别为B1，B2，左、右焦点分别为F1，F2．原点到直线A2B2的距离为$\frac{2\sqrt{5}}{5}$．