题目内容
如图,已知三棱锥O—ABC的侧棱OA、OB、OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.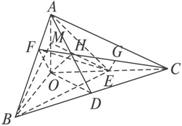
(1)求O点到面ABC的距离;
(2)求异面直线BE与AC所成的角;
(3)求二面角E-AB-C的大小.
解法一:(1)取BC的中点D,连结AD、OD.

∵OB=OC,则OD⊥BC、AD⊥BC,
∴BC⊥面OAD.
过O点作OH⊥AD于H,
则OH⊥面ABC,OH的长就是所要求的距离.
BC=![]() ,OD=
,OD= ![]() .
.
∵OA⊥OB, OA⊥OC,
∴OA⊥面OBC,则OA⊥OD.
AD=![]() ,在Rt△OAD中,有OH=
,在Rt△OAD中,有OH=![]() .
.
(另解:由V=![]() S△ABC·OH=
S△ABC·OH=![]() OA·OB·OC=
OA·OB·OC=![]() ,知OH=
,知OH=![]() )
)
(2)取OA的中点M,连结EM、BM,则EM∥AC,
∠BEM是异面直线BE与AC所成的角.
求得EM=![]() AC=
AC=![]() ,BE=
,BE=![]() ,
,
BM=![]() .cos∠BEM=
.cos∠BEM=![]() ,
,
∴∠BEM=arccos![]() .
.
(3)连结CH并延长交AB于F,连结OF、EF.
∵OC⊥面OAB,∴OC⊥AB.
又∵OH⊥面ABC,∴CF⊥AB,EF⊥AB.
则∠EFC就是所求二面角的平面角.
作EG⊥CF于G,则EG=![]() OH=
OH=![]() .
.
在Rt△OAB中,OF=![]() =
=![]() ,
,
在Rt△OEF中,EF=![]() ,sin∠EFG=
,sin∠EFG=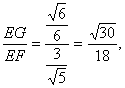
∠EFG=arcsin![]() (或表示为arccos
(或表示为arccos![]() ).
).
解法二:(1)以O为原点,OB、OC、OA分别为x、y、z轴建立空间直角坐标系.
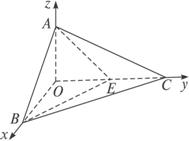
则有A(0,0,1)、B(2,0,0)、C(0,2,0)、E(0,1,0).
设平面ABC的法向量为n1=(x,y,z),
则由n1⊥![]() 知n1·
知n1·![]() =2x-z=0;
=2x-z=0;
由n1⊥![]() 知n1·
知n1·![]() =2y-z=0.
=2y-z=0.
取n1=(1,1,2),则点O到面ABC的距离为d=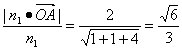 .
.
(2) ![]() =(2,0,0)-(0,1,0)=(2,-1,0),
=(2,0,0)-(0,1,0)=(2,-1,0),![]() =(0,2,-1).
=(0,2,-1).
cos〈![]() ,
,![]() 〉=
〉=![]() =
=![]() ,
,
所以异面直线BE与AC所成的角为arccos![]() .
.
(3)设平面EAB的法向量为n=(x,y,z),
则由n⊥![]() 知n·
知n·![]() =2x-z=0;
=2x-z=0;
由n⊥![]() 知n·
知n·![]() =2x-y=0.
=2x-y=0.
取n=(1,2,2).
由(1)知平面ABC的法向量为n1=(1,1,2).
cos〈n,n1〉=![]() ,
,
结合图形可知,二面角EABC的大小为arccos![]() .
.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 如图,已知三棱锥O-ABC中,
如图,已知三棱锥O-ABC中,| OA |
| a |
| OB |
| b |
| OC |
| c |
| AG |
A、
| ||||||||||
B、-
| ||||||||||
C、
| ||||||||||
D、-
|
 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点. 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点. 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点. 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=2,OB=2,OC=4,E是OC的中点,求二面角E-AB-C的余弦值.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=2,OB=2,OC=4,E是OC的中点,求二面角E-AB-C的余弦值.