题目内容
19.已知函数f(x)=$\left\{\begin{array}{l}{|lnx|,0<x≤{e}^{3}}\\{-x+{e}^{3}+3,x>{e}^{3}}\end{array}\right.$,存在x1<x2<x3,f(x1)=f(x2)=f(x3),则$\frac{f({x}_{3})}{{x}_{2}}$的最大值为$\frac{1}{e}$.分析 作出f(x)的函数图象,得出x1,x2,x3的关系和范围,从而计算出答案.
解答 解:作出f(x)的函数图象如图所示: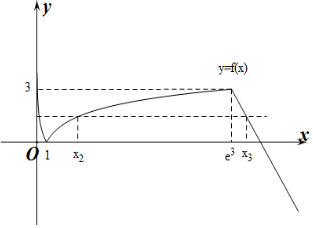
∵存在x1<x2<x3,f(x1)=f(x2)=f(x3),
∴1$<{x}_{2}<{e}^{3}$,
∴$\frac{f({x}_{3})}{{x}_{2}}$=$\frac{f({x}_{2})}{{x}_{2}}$=$\frac{ln{x}_{2}}{{x}_{2}}$,
令g(x)=$\frac{lnx}{x}$,x∈(1,e3),则g′(x)=$\frac{1-lnx}{{x}^{2}}$,
∴当1<x<e时,g′(x)>0,当e<x<e3时,g′(x)<0,
∴g(x)在(1,e)上单调递增,在(1,e3)上单调递减,
∴当x=e时,g(x)取得最大值g(e)=$\frac{1}{e}$.
∴$\frac{ln{x}_{2}}{{x}_{2}}$的最大值为$\frac{1}{e}$.
故答案为$\frac{1}{e}$.
点评 本题考查了函数的单调性判断,函数最值的计算,找出x2的范围,构造函数g(x)是关键,属于中档题.

练习册系列答案
相关题目
9.曲线$\sqrt{2}$ρ=4sin(x+$\frac{π}{4}$)与曲线$\left\{\begin{array}{l}{x=\frac{1}{2}-\frac{\sqrt{2}}{2}t}\\{y=\frac{1}{2}+\frac{\sqrt{2}}{2}t}\end{array}\right.$的位置关系是( )
| A. | 相交过圆心 | B. | 相交 | C. | 相切 | D. | 相离 |
10.满足条件|z-i|+|z+i|=4的复数z在复平面上对应点的轨迹是( )
| A. | 一条直线 | B. | 两条直线 | C. | 圆 | D. | 椭圆 |
4.已知△ABC中,内角A,B,C的对边分别为a,b,c,b=2,B=45°,若三角形有两解,则a的取值范围是( )
| A. | a>2 | B. | 0<a<2 | C. | 2<a<2$\sqrt{2}$ | D. | 2<a<2$\sqrt{3}$ |
9.设函数f(x)在点x0附近有定义,且有f(x0+△x)-f(x0)=a△x+b(△x)2,其中a,b为常数,则( )
| A. | f'(x)=a | B. | f'(x)=b | C. | f'(x0)=a | D. | f'(x0)=b |