题目内容
已知抛物线D的顶点是椭圆C: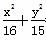 =1的中心,焦点与该椭圆的右焦点重合.
=1的中心,焦点与该椭圆的右焦点重合.
(1) 求抛物线D的方程;
(2) 过椭圆C右顶点A的直线l交抛物线D于M、N两点.
① 若直线l的斜率为1,求MN的长;
② 是否存在垂直于x轴的直线m被以MA为直径的圆E所截得的弦长为定值?如果存在,求出m的方程;如果不存在,说明理由.
解:(1) 由题意,可设抛物线方程为y2=2px(p>0).由a2-b2=4-3=1,得c=1,∴ 抛物线的焦点为(1,0),∴ p=2.
∴ 抛物线D的方程为y2=4x.
(2) 设M(x1,y1),N(x2,y2).
① 直线l的方程为y=x-4,联立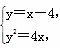 整理得x2-12x+16=0,即M(6-2
整理得x2-12x+16=0,即M(6-2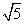 ,2-2
,2-2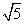 ),N(6+2
),N(6+2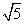 ,2+2
,2+2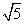 ),
),
∴ MN=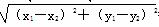 =4
=4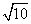 .
.
② 设存在直线m:x=a满足题意,则圆心E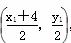 ,过E作直线x=a的垂线,垂足为E′,设直线m与圆E的一个交点为G.可得|E′G|2=|EG|2-|EE′|2,即|E′G|2=|EA|2-|EE′|2=
,过E作直线x=a的垂线,垂足为E′,设直线m与圆E的一个交点为G.可得|E′G|2=|EG|2-|EE′|2,即|E′G|2=|EA|2-|EE′|2=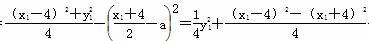 +a(x1+4)-a2=x1-4x1+a(x1+4)-a2=(a-3)x1+4a-a2.当a=3时,|E′G|2=3,此时直线m被以AM为直径的圆E所截得的弦长恒为定值2
+a(x1+4)-a2=x1-4x1+a(x1+4)-a2=(a-3)x1+4a-a2.当a=3时,|E′G|2=3,此时直线m被以AM为直径的圆E所截得的弦长恒为定值2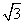 ,因此存在直线m:x=3满足题意.
,因此存在直线m:x=3满足题意.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
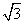 ,求直线l的方程;
,求直线l的方程;

 =1(a>0,b>0)的一个焦点,并与双曲线实轴垂直,已知拋物线与双曲线的一个交点为
=1(a>0,b>0)的一个焦点,并与双曲线实轴垂直,已知拋物线与双曲线的一个交点为 ,求拋物线与双曲线方程.
,求拋物线与双曲线方程. +y2=1上,顶点A与椭圆的焦点F1重合,且椭圆的另外一个焦点F2在BC边上,则△ABC的周长是________.
+y2=1上,顶点A与椭圆的焦点F1重合,且椭圆的另外一个焦点F2在BC边上,则△ABC的周长是________. =1的中心和左焦点,点P为椭圆上的任意一点,则
=1的中心和左焦点,点P为椭圆上的任意一点,则 的最大值为________.
的最大值为________. ,且∠ABC=120°,BC=10,边BC在x轴上且y轴垂直平分BC边,则过点A且以B、C为焦点的双曲线方程为______________.
,且∠ABC=120°,BC=10,边BC在x轴上且y轴垂直平分BC边,则过点A且以B、C为焦点的双曲线方程为______________.