题目内容
已知函数 .
.
(Ⅰ)当 时,讨论
时,讨论 的单调性;
的单调性;
(Ⅱ)若 时
时 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 .
.(Ⅰ)当
 时,讨论
时,讨论 的单调性;
的单调性;(Ⅱ)若
 时
时 恒成立,求
恒成立,求 的取值范围.
的取值范围.解:
(Ⅰ)当 时,
时, ,其定义域为
,其定义域为 .
.
 , ………………………………………2分
, ………………………………………2分
 函数
函数 在
在 ,
, 为减函数,在
为减函数,在 ,
, 为增函数. ……4分
为增函数. ……4分
 (Ⅱ)解:
(Ⅱ)解:
(1)当 时,
时, ,故
,故 ,
,
 ,
, ,函数
,函数 在
在
 增函数,
增函数,
故 ,不合题意,所以
,不合题意,所以 . ………………………6分
. ………………………6分
(2)若 ,此时
,此时 ,
,
①当 时,
时, ,
, 时,
时, ,
,
故 在
在 为减函数,从而
为减函数,从而 恒成立.………………………8
恒成立.………………………8 分
分
②当 时,
时, ,
,
函数 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
则在 上存在
上存在 ,使
,使 ,故不符
,故不符 合题意.
合题意.
③当 时,
时, ,
,  .
.
函数
 在
在 上单调递减,在
上单调递减,在 、
、 上单调递增,
上单调递增,
则在 、
、 上存在
上存在 ,使
,使 ,故不符合题意.
,故不符合题意.
综上, . ………………………………………………………12分
. ………………………………………………………12分
(Ⅰ)当
 时,
时, ,其定义域为
,其定义域为 .
. , ………………………………………2分
, ………………………………………2分 函数
函数 在
在 ,
, 为减函数,在
为减函数,在 ,
, 为增函数. ……4分
为增函数. ……4分 (Ⅱ)解:
(Ⅱ)解:(1)当
 时,
时, ,故
,故 ,
, ,
, ,函数
,函数 在
在
 增函数,
增函数,故
 ,不合题意,所以
,不合题意,所以 . ………………………6分
. ………………………6分(2)若
 ,此时
,此时 ,
,①当
 时,
时, ,
, 时,
时, ,
,故
 在
在 为减函数,从而
为减函数,从而 恒成立.………………………8
恒成立.………………………8 分
分②当
 时,
时, ,
,函数
 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,则在
 上存在
上存在 ,使
,使 ,故不符
,故不符 合题意.
合题意.③当
 时,
时, ,
,  .
.函数

 在
在 上单调递减,在
上单调递减,在 、
、 上单调递增,
上单调递增,则在
 、
、 上存在
上存在 ,使
,使 ,故不符合题意.
,故不符合题意.综上,
 . ………………………………………………………12分
. ………………………………………………………12分略

练习册系列答案
相关题目
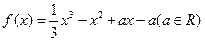 .
.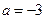 时,求函数
时,求函数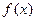 的极值;
的极值; 的扇形,制成一个圆锥形容器,扇形的圆心角
的扇形,制成一个圆锥形容器,扇形的圆心角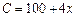 ,月最高产量为150台,出厂单价p(单位:万元)与月产量x的函数关系为
,月最高产量为150台,出厂单价p(单位:万元)与月产量x的函数关系为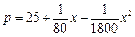 .
. ;
; 的单调递减区间是 .
的单调递减区间是 .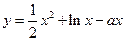 在定义域为增函数,则
在定义域为增函数,则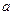 的取值范围是
的取值范围是
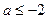

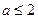
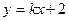 与曲线
与曲线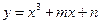 相切于点
相切于点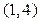 ,则
,则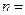 .
. 的图象在点P处的切线方程是
的图象在点P处的切线方程是 ,则
,则 =
= .
. 
 的
的 次幂可用奇数进行如图所示的“分裂”,仿此,记
次幂可用奇数进行如图所示的“分裂”,仿此,记 的“分裂”中的最小数为
的“分裂”中的最小数为 ,而
,而 的“分裂”中最大的数是
的“分裂”中最大的数是 ,则
,则
 .
.