题目内容
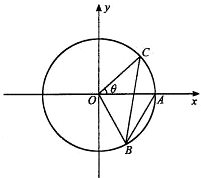
如图，角θ的始边OA落在ox轴上，其始边、终边与单位圆分别交于点A，C，θ∈（0，| π |
| 2 |
| ||
| 5 |
2
| ||
| 5 |
| ||
| 10 |
| ||
| 10 |
分析：由题意利用三角函数的定义可得cos∠COA，sin∠COA，以及∠AOB=
，由cos∠BOC=cos（∠COA+
）通过两角和的余弦函数运算求得结果．
| π |
| 3 |
| π |
| 3 |
解答：解：点C的坐标为（
，
），∴cos∠COA=
，sin∠COA=
．
再由△AOB为等边三角形可得∠AOB=
，
∴cos∠BOC=cos（∠COA+
）
=cos∠COA cos
-sin∠COA sin
=
×
-
×
=
．
故答案为：
．
| ||
| 5 |
2
| ||
| 5 |
| ||
| 5 |
2
| ||
| 5 |
再由△AOB为等边三角形可得∠AOB=
| π |
| 3 |
∴cos∠BOC=cos（∠COA+
| π |
| 3 |
=cos∠COA cos
| π |
| 3 |
| π |
| 3 |
=
| ||
| 5 |
| 1 |
| 2 |
2
| ||
| 5 |
| ||
| 2 |
=
| ||
| 10 |
故答案为：
| ||
| 10 |
点评：本题主要考查三角函数的定义，两角和差的余弦公式的应用，考查计算能力，属于中档题．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
如图，以Ox为始边作任意角α，β，它们的终边与单位圆分别交于A，B点，则
•
的值等于（ ）
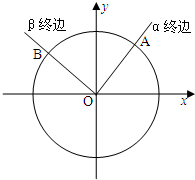
| OA |
| OB |
| A、sin（α+β） |
| B、sin（α-β） |
| C、cos（α+β） |
| D、cos（α-β） |
如图，角θ的始边OA落在ox轴上，其始边、终边与单位圆分别交于点A、C、θ∈（0，
（2012•嘉定区三模）如图，角θ的始边OA落在x上轴，其始边、终边分别与单位圆交于点A、C（0＜θ＜