题目内容
设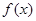 是定义在
是定义在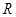 上的函数,且
上的函数,且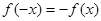 ,当
,当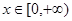 时,
时,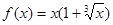 ,那么当
,那么当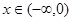 时,
时,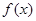 = .
= .
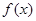 是定义在
是定义在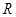 上的函数,且
上的函数,且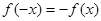 ,当
,当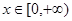 时,
时,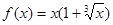 ,那么当
,那么当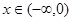 时,
时,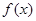 = .
= .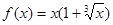
试题分析:根据题意,由于函数
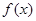 是定义在
是定义在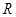 上的函数,且
上的函数,且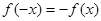 ,说明是偶函数,同时能根据当当
,说明是偶函数,同时能根据当当 ,因此可知
,因此可知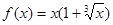 ,
,点评:解决的关键是将变量转换到已知区间来求解解析式,对称性的运用,属于基础题。

练习册系列答案
相关题目
题目内容
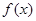 是定义在
是定义在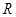 上的函数,且
上的函数,且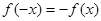 ,当
,当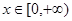 时,
时,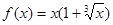 ,那么当
,那么当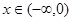 时,
时,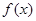 = .
= .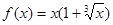
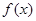 是定义在
是定义在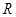 上的函数,且
上的函数,且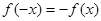 ,说明是偶函数,同时能根据当当
,说明是偶函数,同时能根据当当 ,因此可知
,因此可知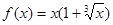 ,
,